Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào ha
Lưu về Facebook:
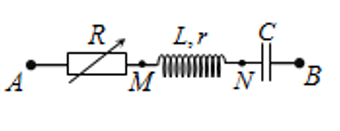
MỤC LỤC
Câu hỏi:
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch (hình dưới). Điều chỉnh đến giá trị 80 thì công suất tiêu thụ trên biến trở đạt cực đại, đồng thời tổng trở của đoạn mạch là số nguyên nhỏ nhất và chia hết cho 40. Khi đó, hệ số công suất của đoạn mạch có giá trị là
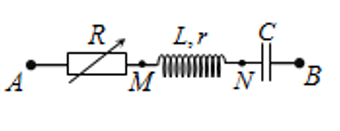
Đáp án án đúng là: C
Lời giải chi tiết:
+ Để công suất trên biến trở là cực đại
→ Tổng trở của mạch khi đó
+ Để chia hết cho 40 thì số nguyên, vậy chỉ có thể là một bội số của 10
→ Hệ số công suất của đoạn MB
chỉ có đáp án A và D là thỏa mãn.
+ Lập bảng →
→ Đáp án C
Xem thêm các bài tiếp theo bên dưới
- Đặt điện áp V ($\Lar
- Cho mạch điện xoay chiều như hình vẽ, trong đó giá trị biến trở R và đ
- Từ một trạm phát điện xoay chiều một pha đặt tại vị trí M, điện năng đ
- Mạch điện nối tiếp AB (như hình 1) với với $\Large\ 0 < R_1 \leqslant
- Một sóng cơ học có tần số f = 1000 Hz lan truyền trong không khí. Sóng