Gọi S là tập hợp các giá trị nguyên của tham số $\Large m$ để đồ thị h

Gọi S là tập hợp các giá trị nguyên của tham số $\Large m$ để đồ thị hàm số $\Large y=\dfrac{\sqrt{x+2}}{\sqrt{x^2-6x+2m}}$ có hai đường tiệm cận đứng. Số phần tử của tập S là

• A. Vô số.
• B. 12.
• C. 14.
• D. 13.

Hàm số xác định khi: $\Large \left\{\begin{align} & x+2\geq 0 \\ & x^2-6x+2m > 0 \end{align}\right.$

Điều kiện để đồ thị hàm số đã cho có hai đường tiệm cận đứng là phương trình

$\Large x^2-6x+2m=0$ có hai nghiệm phân biệt $\Large x_1; x_2 > -2$.

Ta có: $\Large x^2-6x+2m=0$ $\Large \Leftrightarrow -x^2+6x=2m$ (*)

Xét hàm số: $\Large f(x)=-x^2+6x$ trên $\Large (-2; +\infty)$.

Bảng biến thiên:

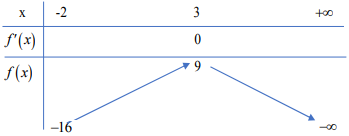
Từ bảng biến thiên suy ra phương trình (*) có hai nghiệm phân biệt $\Large x_1; x_2 > -2$ khi $\Large -16 < 2m < 9$ $\Large \Leftrightarrow -8 < m < \dfrac{9}{2}$.

Vậy có 12 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.