Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí

Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu $\large V_{1}, V_{2}$ lần lượt là thể tích của hình nón và thể tích của khối cầu nội tiếp hình nón. Giá trị bé nhất của tỉ số $\large \dfrac{V_{1}}{V_{2}}$ là:

• A. A. $\large \dfrac{5}{4}$
• B. B. $\large \dfrac{4}{3}$
• C. C. 3
• D. D. 2

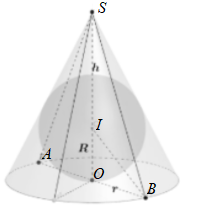
Ta có: Thể tích khối nón là $\large V_{1} = \dfrac{1}{3}\pi r^{2}h$ 

Xét (SAB) là mặt cắt qua tâm, kẻ tia phân giác của góc $\large \widehat{SBO}$, cắt SO tại I.

Ta có: 

$\large \dfrac{IO}{IS} = \dfrac{OB}{SB} = \dfrac{r}{\sqrt{r^{2}+h^{2}}}\Rightarrow IS = IO.\dfrac{\sqrt{r^{2}+h^{2}}}{r}$ 

Mặt khác: IO + IS = h

Do đó ta có bán kính của mặt cầu nội tiếp hình chóp là 

$\large R = IO = \dfrac{rh}{r+\sqrt{r^{2}+h^{2}}}$ 

Thể tích khối cầu là 

$\large V_{2} = \dfrac{4}{3}\pi R^{3} = \dfrac{4}{3}\pi \dfrac{r^{3}h^{3}}{\left (r+\sqrt{r^{2}+h^{2}}  \right )^{3}}$ 

$\large \Rightarrow \dfrac{V_{1}}{V_{2}}= \dfrac{\left (r+\sqrt{r^{2}+h^{2}}  \right )^{3}}{4rh^{2}}= \dfrac{\left (1+\sqrt{1+\dfrac{h^{2}}{r^{2}}}  \right )^{3}}{4\dfrac{h^{2}}{r^{2}}}$ 

Đặt $\large t = \sqrt{1+\dfrac{h^{2}}{r^{2}}}$ $\large (t\geq 1)\Rightarrow \dfrac{V_{1}}{V_{2}}=\dfrac{(1+t)^{3}}{4(t^{2}-1)}=\dfrac{(t+1)^{2}}{4(t-1)}$ 

Đặt f(t) = $\large \dfrac{(t+1)^{2}}{t-1}$. Điều kiện: $\large (t > 1)$ 

$\large f'(t)=\dfrac{t^{2}-2t-3}{(t-1)^{2}}$, f’(t) = 0 $\large \Leftrightarrow$ t = 3, f(3) = 8

$\large\Rightarrow f(t)\geq 8\forall t > 1 \Rightarrow \dfrac{V_{1}}{V_{2}}\geq 2$ 

Chọn D