Cho nửa đường tròn đường kính AB = 2 R , hai điểm C, D di động trên nử

Cho nửa đường tròn đường kính AB = 2R, hai điểm C, D di động trên nửa đường tròn sao cho CD // AB. Kí hiệu CD = x, tìm x để vật thể tròn xoay tạo thành khi quay hình thang cân ACDB quanh trục AB lớn nhất.

• A.

  A. $\large x = \dfrac{R(\sqrt{13}-1)}{3}$

• B.

  B. $\large x = \dfrac{2R}{\sqrt{3}}$

• C.

  C. $\large x = \dfrac{R(1+2\sqrt{13})}{15}$

• D.

  D. $\large x = \dfrac{R}{\sqrt{3}}$

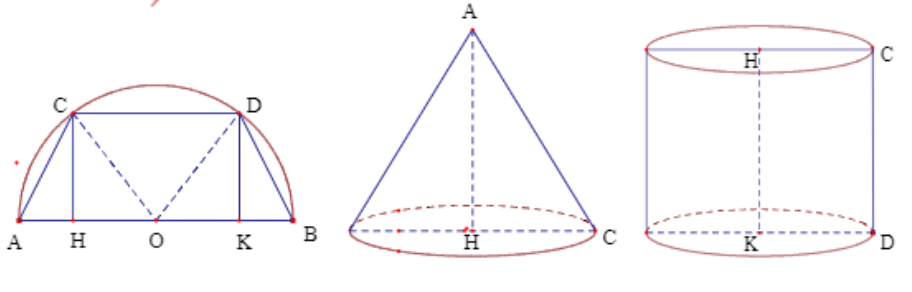
Chọn A

Kí hiệu $\large \widehat{COD} = 2\alpha \Rightarrow \widehat{COA} = \widehat{DOB} = 90^{\circ}-\alpha$ và H, K lần lượt là hình chiếu vuông góc của C, D lên AB.

Ta có $\large CD = HK = 2Rsin\alpha$ và

$\large OH = OK = \dfrac{HK}{2}  = Rsin\alpha$, 

$\large AH = KB = \dfrac{2R-2Rsin\alpha }{2} = R-Rsin\alpha$ 

Khi quay hình thang cân ACDB quanh trục AB ta được khối tròn xoay có thể tích bằng tổng thể tích của khối trụ có:

$\large r = CH = \sqrt{OC^{2}-OH^{2}} = \sqrt{R^{2}-R^{2}sin^{2}\alpha} = R.cos\alpha$ 

$\large h = HK = 2R.sin\alpha$ 

và thể tích của hai khối nón bằng nhau có 

$\large r = CH = R.cos\alpha$, $\large h = AH = R-Rsin\alpha$ 

Vì vậy $\large V = \pi R^{2}.cos^{2}\alpha .2R.sin\alpha + \dfrac{2\pi R^{2}.cos^{2}\alpha.(R-R.sin\alpha)}{3}$ 

$\large = \dfrac{2\pi R^{3}.cos^{2}\alpha .(3.sin\alpha+1-sin\alpha)}{3}$ 

$\large = \dfrac{2\pi R^{3}.(1+2sin\alpha ).(1-sin^{2}\alpha)}{3}\leq \dfrac{35+13\sqrt{13}}{81}\pi R^{3}$ 

Dấu bằng đạt tại 

$\large sin\alpha = \dfrac{\sqrt{13}-1}{6}\Rightarrow CD = 2Rsin\alpha  = \dfrac{R(\sqrt{13}-1)}{3}$. 

Chú ý: Khảo sát hàm số $\large f(x) = \dfrac{2.(1+2x).(1-x^{2})}{3}$ trên đoạn [0;1] , ta có

$\large \underset{[0;1]}{max}f(x) = f\left (\dfrac{\sqrt{13}-1}{6}  \right ) = \dfrac{35+13\sqrt{13}}{81}$