Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AD = 2 a ,

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AD = 2a, AB = BC = CD = a. Cạnh bên SA = 2a và vuông góc với đáy. Gọi R là bán kính mặt cầu ngoại tiếp khối chóp S.ABCD. Tỉ số $\large \dfrac{R}{a}$ nhận giá trị nào sau đây?
Đáp án án đúng là: D
Lời giải chi tiết:
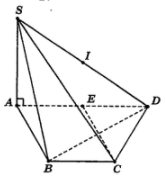
Ta có SA $\large \perp$AD hay $\large \widehat{SAD} = 90^{\circ}$.
Gọi E là trung điểm AD.
Ta có EA = AB = BC nên ABCE là hình thoi.
Suy ra CE = EA = $\large \dfrac{1}{2}$AD.
Do đó tam giác ACD vuông tại C. Ta có:
$\large \left\{\begin{matrix}
DC \perp AC & \\
DC \perp SA &
\end{matrix}\right.\Rightarrow DC \perp (SAC)\Rightarrow DC \perp SC$ hay $\large \widehat{SCD} = 90^{\circ}$
Tương tự, ta cũng có SB $\large \perp$BD hay $\large \widehat{SBD} = 90^{\circ}$
Ta có $\large \widehat{SAD} = \widehat{SBD} = \widehat{SCD} = 90^{\circ}$ nên khối chóp S.ABCD nhận trung điểm I của SD làm tâm mặt cầu ngoại tiếp, bán kính:
$\large R = \dfrac{SD}{2} = \dfrac{\sqrt{SA^{2}+AD^{2}}}{2} = a\sqrt{2}$
Suy ra $\large \dfrac{R}{a} = \sqrt{2}$. Chọn D.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , BD = a . Hình c
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và AB = AC = a
- Cho hình nón có bán kính đáy là 5 a , độ dài đường sinh là 13 a . Thể
- Một hình thang cân có chiều cao h và độ dài hai đáy là a, b . Tính thể
- Cho hình nón đỉnh S , đáy là hình tròn tâm O , góc ở đỉnh bằng $\large