Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , BD = a . Hình c

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng $\large 60^{\circ}$. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
Đáp án án đúng là: C
Lời giải chi tiết:
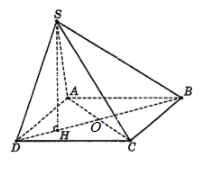
Ta có $\large 60^{\circ}=(\widehat{SD,(ABCD)})=(\widehat{SD,HD})=\widehat{SDH}$
Trong tam giác vuông SHD, có
$\large SH = DH.tan\widehat{SDH} = \dfrac{BD}{4}.tan\widehat{SDH} = \dfrac{a\sqrt{3}}{4}$ và
$\large SD = \dfrac{HD}{cos\widehat{SDH}} = \dfrac{a}{2}$
Trong tam giác vuông SHB, có
$\large SB = \sqrt{SH^{2}+HB^{2}}=\dfrac{a\sqrt{3}}{2}$.
Xét tam giác SBD, ta có $\large SB^{2}+SD^{2} = a^{2} = BD^{2}$.
Suy ra tam giác SBD vuông tại S.
Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là O, bán kính $\large R = \dfrac{1}{2}BD = \dfrac{a}{2}$. Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và AB = AC = a
- Cho hình nón có bán kính đáy là 5 a , độ dài đường sinh là 13 a . Thể
- Một hình thang cân có chiều cao h và độ dài hai đáy là a, b . Tính thể
- Cho hình nón đỉnh S , đáy là hình tròn tâm O , góc ở đỉnh bằng $\large
- Cho một khối trụ có bán kính đáy r = a và chiều cao h = 2a . Mặt phẳng