Trong mặt phẳng ( P ) cho tam giác ABC đều cạnh bằng 8 cm và một điểm

Trong mặt phẳng (P) cho tam giác ABC đều cạnh bằng 8 cm và một điểm S di động ngoài mặt phẳng (P) sao cho tam giác MAB luôn có diện tích bằng $\large 16\sqrt{3}$ $\large cm^{2}$, với M là trung điểm của SC. Gọi (S) là mặt cầu đi qua bốn đỉnh M, A, B, C. Khi thể tích hình chóp S.ABC lớn nhất, tính bán kính nhỏ nhất của (S):

 

• A. A. $\large \dfrac{16\sqrt{6}}{9}$ cm
• B. B. $\large \dfrac{4\sqrt{3}}{3}$ cm
• C. C. $\large \dfrac{4\sqrt{15}}{3}$ cm
• D. D. $\large \dfrac{4\sqrt{39}}{3}$ cm

Chọn C

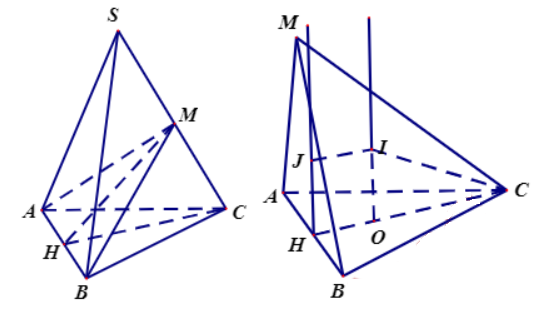
Gọi H là trung điểm cạnh AB, ta có: CH $\large \perp$AB.

Ta có: $\large d(S,(ABC)) = 2d(M,(ABC))\Rightarrow V_{S.ABC} = 2V_{M.ABC}$ 

Mà:

$\large V_{M.ABC} = V_{C.MAB} = \dfrac{1}{3}S_{\Delta MAB}.d(C,(MAB))$

= $\large \dfrac{1}{3}.16\sqrt{3}.d(C,(MAB))\leq \dfrac{1}{3}.16\sqrt{3}.CH$

Do đó, $\large V_{S.ABC}$ lớn nhất khi và chỉ khi d(C,(MAB)) = CH hay CH $\large \perp$(MAB).

Gọi J, O lần lượt là tâm hai đường tròn ngoại tiếp hai tam giác MAB và tam giác ABC.

Dựng hai trục của hai đường tròn ngoại tiếp hai tam giác MAB và tam giác ABC cắt nhau tại I. Khi đó I chính là tâm mặt cầu ngoại tiếp đi qua 4 điểm A, B, C, M và bán kính mặt cầu đi qua bốn điểm A, B, C, M là 

$\large R = CI = \sqrt{OC^{2}+OI^{2}} = \sqrt{\left (\dfrac{8\sqrt{3}}{3}  \right )^{2}+JH^{2}}$ 

Do $\large S_{\Delta MAB} = 16\sqrt{3}$, AB = 8 $\large \Rightarrow d(M,AB) = 4\sqrt{3}$.

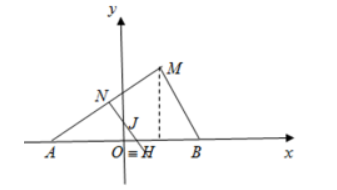
Chọn hệ trục tọa độ Oxy như hình vẽ, ta có H(0;0), A(-4;0), B(4;0), M(a;$\large 4\sqrt{3}$).

Đường trung trực của đoạn thẳng AM đi qua điểm $\large N\left (\dfrac{a-4}{2};2\sqrt{3}  \right )$ và có một véc tơ pháp tuyến $\large \overrightarrow{AM} = (a+4;4\sqrt{3})$ nên có phương trình là:

$\large (a+4)\left (x-\frac{a-4}{2}  \right )+4\sqrt{3}(y-2\sqrt{3})= 0$ 

J là giao điểm của trục tung và đường trung trực của AM

$\large \Rightarrow J\left (0;\dfrac{a^{2}+32}{8\sqrt{3}}  \right )\Rightarrow JH = \dfrac{a^{2}+32}{8\sqrt{3}}\geq \dfrac{4\sqrt{3}}{3}$ 

Do đó:

$\large R_{min} = \sqrt{\left (\dfrac{8\sqrt{3}}{3}  \right )^{2}+\left (\dfrac{4\sqrt{3}}{3}  \right )^{2}} = \dfrac{4\sqrt{15}}{3}$.