Giả sử hàm số $\large y=mx^4-(m^2+2)x^2+\dfrac{m^3+11m}{9}$ có đồ thị

Giả sử hàm số $\large y=mx^4-(m^2+2)x^2+\dfrac{m^3+11m}{9}$ có đồ thị (C) và hàm số $\large y=x^2$ có đồ thị (C') cắt nhau tại bốn điểm phân biệt. Biết rằng hình phẳng (H) giới hạn bởi (C) và (C') là hợp của ba hình phẳng $\large (H_1), \, (H_2), \, (H_3)$ có diện tích tương ứng là $\large S_1, \, S_2, \, S_3$ trong đó $\large 0 <  S_1\leq S_2\leq S_3$ và các hình phẳng $\large (H_1), \, (H_2), \, (H_3)$ đôi một giao nhau tại không quá một điểm. Gọi T là tập hợp các giá trị của m sao cho $\large S_3=S_1+S_2$. Tính tổng bình phương các phần tử của T

• A. 23
• B. 14
• C. 20
• D. 19

Chọn B

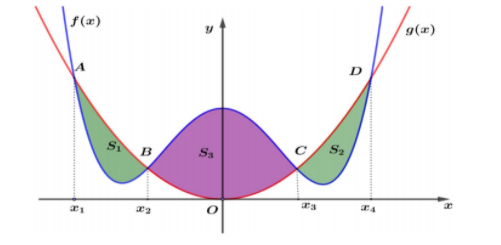
Đặt $\large f(x)=mx^4- (m^2+2)x^2+\dfrac{m^3+11m}{9}; g(x)=x^2$

+) Để đồ thị (C) cắt (C') theo 4 điểm phân biệt thỏa mãn yêu cầu bài toán thì đồ thị (C) phải có 3 điểm cực trị 

$\large \Leftrightarrow a.b<0 \Leftrightarrow m\left[ -(m^2+2)\right] <0\Leftrightarrow m>0$

+) Phương trình tương giao của (C) và (C') là: $\large f(x)-g(x)=0$

$\large mx^4-(m^2+3) x^2+\dfrac{m^3+11m}{9}=0 $ (1) có 4 nghiệm phân biệt $\large x_1, \, x_2, \, x_3, \, x_4$

+) Hàm số $\large h(x)=f(x)-g(x)$ là hàm số chẵn nên $\large S_1=S_2$. Suy ra: $\large S_3=2S_2\Leftrightarrow S_2=\dfrac{S_3}{2}$

+) Ta có: $\large \dfrac{S_3}{2}=\int^{x_3}_0\left[f(x)-g(x) \right ]dx; \,\, S_2=-\int_{x_3}^{x_4}\left[f(x)-g(x) \right ]dx$. Khi đó ta có: 

$\large \int^{x_3}_0\left[f(x)-g(x) \right ]dx=-\int_{x_3}^{x_4}\left[f(x)-g(x) \right ]dx \Leftrightarrow \int_0^{x_3}[f(x)-g(x)]dx+ \int_{x_3}^{x_4}[f(x)-g(x)]dx=0$

$\large \Leftrightarrow \int_0^{x_4}[f(x)-g(x)]dx= 0\Leftrightarrow \int_0^{x_4}\left[mx^4-(m^2+3)x^2+\dfrac{m^3+11m}{9} \right ]=0$ 

$\large \Leftrightarrow m.\dfrac{x^5_4}{5}-(m^2+3).\dfrac{x_4^3}{3}+\left(\dfrac{m^3+11m}{9} \right )x_4=0\Leftrightarrow \left[\begin{align}& x_4=0\,\, (L)\\& m.\dfrac{x^4_4}{5}-(m^2+3).\dfrac{x_4^2}{3}+\dfrac{m^3+11m}{9} =0\,\, (2)\\\end{align}\right. $ 

+) Từ (1) suy ra: $\large \dfrac{m^3+11m}{9}=-mx^4_4+(m+3)x_4^2\,\, (3)$

+) Thay (3) vào (2) ta có: $\large \dfrac{4m}{5}x_4^4-\dfrac{2(m^2+3)}{3}x_4^2=0\Leftrightarrow x_4^2=\dfrac{5(x^2+3)}{6m}, (\text {do}\,\, x_4\neq 0)\,\, (4)$ 

+) Thay (4) vào (2) ta có: $\large \dfrac{m}{5}\left[\dfrac{5(m^2+3)}{6m} \right ]^2-\dfrac{(m^2+3)}{3}.\dfrac{5(m^2+3)}{6m}+\dfrac{m^3+11m}{9}=0$

$\large \Leftrightarrow \dfrac{5(m^2+3)^2}{36m}-\dfrac{5(m^2+3)^2}{18m}+\dfrac{m^3+11m}{9}=0\Leftrightarrow 5(m^2+3)^2=4m(m^3+11m)$

$\large \Leftrightarrow m^4-14m^2+45=0\Leftrightarrow $ $\large \left[\begin{align}& m^2=9\\& m^2=5\\\end{align}\right.$ $\large \Leftrightarrow \left[\begin{align}& m=3\\& m=\sqrt{5}\\\end{align}\right. $ ( do m > 0)

Suy ra: $\large T=\left\{3, \sqrt{5}\right\}\Rightarrow 3^2+(\sqrt{5})^2=14$