Cho $\large y=f(x)$ là hàm số đa thức bậc bốn và có đồ thị của hàm số

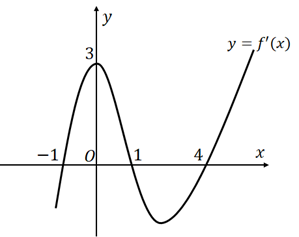
Cho $\large y=f(x)$ là hàm số đa thức bậc bốn và có đồ thị của hàm số $\large y=f'(x)$ như hình vẽ dưới đây.

Hàm số $\large y=f\left(|2-x|\right)$ có bao nhiêu điểm cực tiểu?

• A. 5
• B. 4
• C. 3
• D. 2

Có $\large y'=[f(|2-x|)]=(|2-x|)'.f'(|2-x|)=-\dfrac{(2-x)}{|2-x|}.f'(|2-x|)=\dfrac{x-2}{|2-x|}.f'(|2-x|)$

Dựa vào đồ thị như hình vẽ suy ra

$\large \begin{align} y'=\dfrac{x-2}{|2-x|}.k(|2-x|+1)(|2-x|-1)(|2-x|-4); \,\, k>0\\=k.\dfrac{x-2}{|2-x|}.(|2-x|+1).\dfrac{\left(|2-x|^2-1^2 \right )\left(|2-x|^2-4^2 \right )}{(|2-x|+1)(|2-x|+4)}\\=k.\dfrac{x-2}{|2-x|}.\dfrac{(1-x)(3-x)(-2-x)(6-x)}{|2-x|+4}; \,\, k>0\\
y'=0\Leftrightarrow x=1; x=2; x=-2; x=3; x=6 \\\end{align}$

Từ đó, ta có bảng xét dấu:

Vậy hàm số $\large y=f(|2-x|)$ có 3 điểm cực tiểu.