Cho khối tứ diện ABCD có thể tích bằng 2020. Gọi A', B', C', D' lần lư

Cho khối tứ diện ABCD có thể tích bằng 2020. Gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Tính thể tích V của khối tứ diện A'B'C'D'

• A.

  $\large V=\dfrac{2020}{27}$

• B.

  $\large V=\dfrac{505}{2}$

• C.

  $\large V=\dfrac{505}{4}$

• D.

  $\large V=\dfrac{505}{16}$

Chọn A

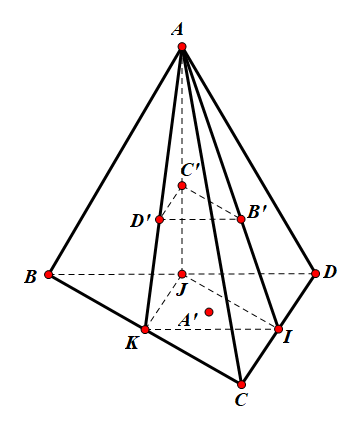
Gọi I, J, K lần lượt là trung điểm của CD, BD, BC

Ta có:

$\large \left\{\begin{align}& B'C'//IJ, \,\, B'C'=\dfrac{2}{3}IJ\\& C'D'// JK,\, C'D'=\dfrac{2}{3}JK\\& B'D'//IK,\, B'D'=\dfrac{2}{3}IK\\\end{align}\right. $ $\large \Rightarrow S_{\Delta B'C'D'}=\left(\dfrac{2}{3} \right )^2S_{\Delta IJK}=\dfrac{4}{9}.\dfrac{1}{4}.S_{\Delta BCD}=\dfrac{1}{9}.S_{\Delta BCD}$

Vì $\large (B'C'D')//(BCD)\Rightarrow \dfrac{d_{(A, (B'C'D'))}}{d_{(A, (BCD))}}=\dfrac{AB'}{AI}=\dfrac{2}{3}\Rightarrow d_{(A, (B'C'D'))}=\dfrac{2}{3}d_{(A, (BCD))}$ 

Suy ra: 

$\large d_{(A',(B'C'D'))}=d_{(A, (BCD))}-d_{(A, (B'C'D'))}=d_{(A, (BCD))}-\dfrac{2}{3}d_{(A, (BCD))}=\dfrac{1}{3}d_{(A, (BCD))}$

Vậy $\large V_{A'B'C'D'}=\dfrac{1}{3}d_{(A', (B'C'D'))}.S_{\Delta B'C'D'}=\dfrac{1}{3}.\dfrac{1}{3}.d_{(A, (BCD))}.\dfrac{1}{9}.S_{\Delta BCD}=\dfrac{1}{27}V_{ABCD}=\dfrac{2020}{27}$