Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số dưới đ

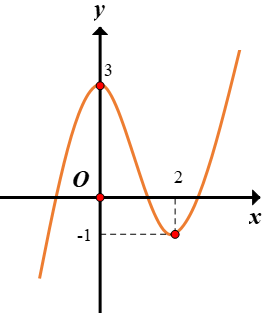
Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số dưới đây. Hỏi hàm số đó là hàm số nào?

• A. A. $y=-{{x}^{3}}+3{{x}^{2}}+3$
• B. B. $y=-{{x}^{3}}-3{{x}^{2}}+3$
• C. C. $y={{x}^{3}}-3x+3$
• D. D. $y={{x}^{3}}-3{{x}^{2}}+3$

Xét hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ với $a=1$ hoặc $a=-1$
Ta có $y'=3a{{x}^{2}}+2bx+c$
Dựa vào đồ thị hàm số ta có $a>0$$\Rightarrow a=1$, lại có $y\left( 0 \right)=3\Rightarrow d=3$
Hàm số có 2 điểm cực trị $x=0$ và $x=2$ nên ta có
 $\left\{ \begin{matrix}   & y'\left( 0 \right)=0 \\   & y'\left( 2 \right)=0 \\  \end{matrix} \right.$$\Leftrightarrow \left\{ \begin{matrix}   & c=0 \\   & 12a+4b+c=0 \\  \end{matrix} \right.$$\Leftrightarrow \left\{ \begin{matrix}   & c=0 \\   & b=-3 \\  \end{matrix} \right.$
Suy ra hàm số cần tìm là $y={{x}^{3}}-3{{x}^{2}}+3$
Chọn đáp án D.