Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$, đồ thị củ

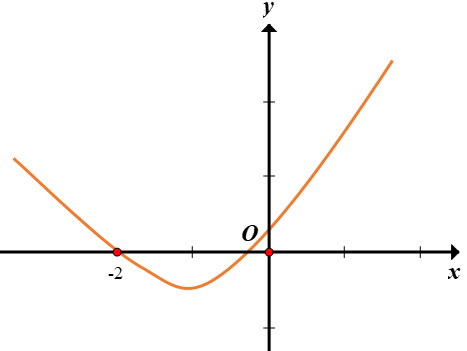
Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$, đồ thị của đạo hàm $f'\left( x \right)$ như hình vẽ bên . Trong các mệnh đề sau, mệnh đề nào sai?

• A. A. $f$ đạt cực tiểu tại $x=-2$
• B. B. $f$ đạt cực tiểu tại $x=0$
• C. C. Cực tiểu của $f$ nhỏ hơn cực đại.
• D. D. $f$ đạt cực đại tại $x=-2$

Lời giải:
Theo giả thiết $f'\left( x \right)$ đổi dấu từ dương sang âm khi $x$ qua $-2$ nên $x=-2$ là điểm cực đại của hàm số $f\left( x \right)$ và $f'\left( x \right)$ đổi dấu từ âm sang dương khi $x$ qua $0$ nên $x=0$ là điểm cực tiểu của hàm số $f\left( x \right)$.
Bảng biến thiên của hàm số $f\left( x \right)$

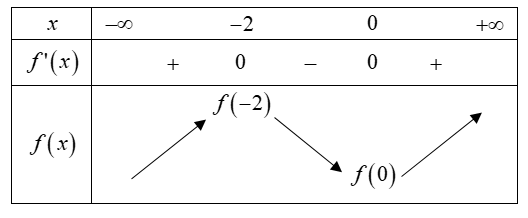
Từ đó ta thấy cực tiểu của $f$ nhỏ hơn cực đại của nó.
Chọn đáp án A