Công ty mĩ phẩm chuẩn bị ra một mẫu sản phẩm dưỡng da mới mang tên Ngọ

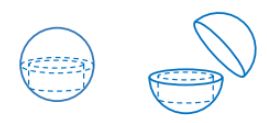
Công ty mĩ phẩm chuẩn bị ra một mẫu sản phẩm dưỡng da mới mang tên Ngọc Trai với thiết kế là một khối cầu như viên ngọc trai khổng lồ, bên trong là một khối trụ nằm trong nửa khối cầu để đựng kem dưỡng (tham khảo hình vẽ dưới). Theo dự kiến, nhà sản xuất có dự định để khối cầu có bán kính là $\large R=3 \sqrt{3} \mathrm{cm}$. Tìm thể tích lớn nhất của khối trụ đựng kem để thể tích thực ghi trên bìa hộp là lớn nhất (với mục đích thu hút khách hàng).

• A.

  A. $\large 54 \pi \mathrm{cm}^{3}$

• B.

  B. $\large 18 \pi \mathrm{cm}^{3}$

• C.

  C. $\large 108 \pi \mathrm{cm}^{3}$

• D.

  D. $\large 45\pi \mathrm{cm}^{3}$

Đây là một bài toán thực tế dựa trên ứng dụng: khối trụ nội tiếp nửa khối cầu. Ta có mặt cắt của nửa khối cầu đựng mĩ phẩm với các kích thước được thể hiện trong hình vẽ sau:

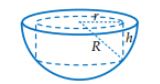
Ý tưởng của bài toán này dựa trên kiến thức chúng ta đã học là tìm GTLN-GTNN của hàm số một biến trên 1 khoảng (đoạn). Ở đây có hai biến đó là r và h. Do đó ta sẽ tìm cách để đưa về một biến, đưa biến này theo biến kia. Ở đây tôi sẽ đưa r theo h.

Ta nhận thấy theo định lý Pytago thì $\large r^{2}=R^{2}-h^{2}$

Khi đó

$\large V_{\text{trụ}}=B h=\pi r^{2} h=\pi\left(R^{2}-h^{2}\right) h=\pi\left(-h^{3}+R^{2} h\right)$

Để thể tích khối trụ lớn nhất thì $\large f(h)=-h^{3}+R^{2} h$ có GTLN trên (0;R).

$\large f^{\prime}(h)=-3 h^{2}+R^{2}=0 \Leftrightarrow h=\dfrac{R}{\sqrt{3}}=\dfrac{3\sqrt{3}}{\sqrt{3}}=3$

Ta có bảng biến thiên:

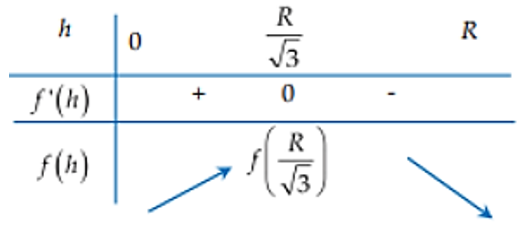
Từ bảng biến thiên suy ra GTLN của hàm số $\Large y=f(h)$ là: $\large f\left(\dfrac{R}{\sqrt{3}}\right)=f(3)=-3^{3}+(3 \sqrt{3})^{2} \cdot 3=54$

Vậy $\large V_{\max }=54 \pi$.