Có một miếng tôn hình tam giác đều $\Large ABC$ cạnh 3dm (như hình vẽ)

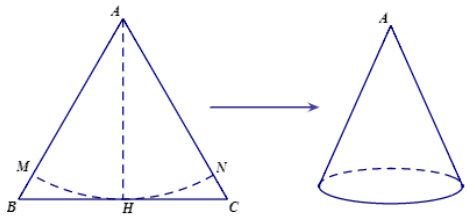
Có một miếng tôn hình tam giác đều $\Large ABC$ cạnh 3dm (như hình vẽ). Gọi $\Large H$ là trung điểm của $\Large BC$. Người ta dùng compa lấy $\Large A$ làm tâm và $\Large AH$ là bán kính để vạch cung tròn $\Large MN$ ($\Large M, N$ theo thứ tự thuộc cạnh $\Large AB$ và $\Large AC$) rồi cắt miếng tôn theo cung tròn đó. Lấy phần hình quạt người ta gò sao cho cạnh $\Large AM$ và $\Large AN$ trùng nhau thành một cái phễu hình nón không đáy với đỉnh $\Large A$. Thể tích cái phễu bằng.

• A. $\Large \dfrac{\sqrt{141}\pi}{64}$ lít.
• B. $\Large \dfrac{3\pi}{32}$ lít.
• C. $\Large \dfrac{\sqrt{105}\pi}{64}$ lít.
• D. $\Large \dfrac{3\sqrt{3}\pi}{32}$ lít.

Chọn C

Độ dài cung tròn $\Large MN$ là $\Large l=2\pi . AH.\dfrac{MAN}{360^{\circ}}=2\pi .\left(AB.\dfrac{\sqrt{3}}{2}\right).\dfrac{MAN}{360^{\circ}}=\dfrac{\pi\sqrt{3}}{2}$.

Mà độ dài cung tròn $\Large MN$ cũng chính là chu vi đáy của cái phễu hình nón, suy ra bán kính của cái phễu là $\Large r=\dfrac{l}{2\pi}=\dfrac{\sqrt{3}}{4}$.

Độ dài đường sinh của cái phễu là $\Large l_N=AH=AB.\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}$. Ta có $\Large h=\sqrt{l_N^2-r^2}=\dfrac{\sqrt{105}}{4}$.

Vậy thể tích của cái phễu đã cho là $\Large V=\dfrac{1}{3}\pi r^2h=\dfrac{\sqrt{105}\pi}{64}$ (lít).