Cho hai số phức $\Large z_1, z_2$ thỏa mãn điều kiện $\Large \left\{\b

Cho hai số phức $\Large z_1, z_2$ thỏa mãn điều kiện $\Large \left\{\begin{align} & |z_1+1+i|=|z_2+1+i|=2\\ & |z_1|+|z_2|=|z_1-z_2| \end{align}\right.$. Biết $\Large z_1$ là số phức có phần thực dương. Khi biểu thức $\Large T=|z_1|+2|z_2|$ đạt giá trị nhỏ nhất thì tích của phần thực và phần ảo của $\Large z_1$ bằng

• A.

  $\Large -\dfrac{3}{2}$.

• B.

  $\Large -\dfrac{5}{4}$.

• C.

  $\Large 3-2\sqrt{2}$.

• D.

  $\Large -2$.

Chọn A

Gọi $\Large A, B$ lần lượt là các điểm biểu diễn các số phức $\Large z_1, z_2$ theo giả thiết $\Large OA+OB=AB$ $\Large \Leftrightarrow O$ thuộc đoạn $\Large AB$.

Ta có $\Large |z_1+1+i|=|z_2+1+i|=2$ $\Large \Leftrightarrow |z_1-(-1-i)|=|z_2-(-1-i)|=2$ $\Large \Rightarrow A, B$ thuộc đường tròn tâm $\Large I(-1; -1)$, $\Large R=2$.

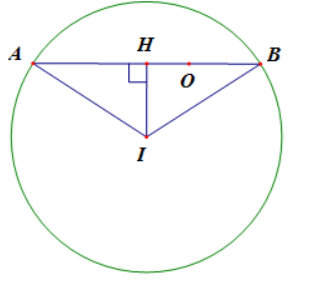
Ta có $\Large T=|z_1|+2|z_2|=OA+2OB$ $\Large \Leftrightarrow T^2=OA^2+4OB^2+4OA.OB=OA^2+4OB^2-4\overrightarrow{OA}.\overrightarrow{OB}$.

Gọi $\Large H$ là trung điểm đoạn $\Large AB$, ta có $\Large \overrightarrow{OA}.\overrightarrow{OB}=\left(\overrightarrow{OH}+\overrightarrow{HA}\right)\left(\overrightarrow{OH}+\overrightarrow{HB}\right)=OH^2-HA^2$ $\Large =OI^2-HI^2-HA^2=OI^2-AI^2=2-4=-2$.

Dấu bằng xảy ra $\Large \Leftrightarrow \left\{\begin{align} & OA^2=4OB^2\\ & OA.OB=2 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & OA=2\\ & OB=1 \end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & |z_1|=2\\ & |z_2|=1 \end{align}\right.$

Đặt $\Large z_1=x+yi$, $\Large (x, y\in\mathbb{R})$ $\Large \Rightarrow \left\{\begin{align} & |z_1+1+i|=2\\ & |z_1|=2\end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align} & (x+1)^2+(y+1)^2=4\\ & x^2+y^2=4\end{align}\right.$

$\Large \Leftrightarrow \left\{\begin{align} & x+y=-1 \\ & x^2+y^2=4 \end{align}\right.$. Suy ra $\Large xy=\dfrac{(x+y)^2-(x^2+y^2)}{2}=\dfrac{(-1)^2-4}{2}=-\dfrac{3}{2}$.