Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông, mặt

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông, mặt bên $\Large (SAB)$ là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy $\Large (ABCD)$ và có diện tích bằng $\Large \dfrac{{27\sqrt 3 }}{4}$ (đvdt). Một mặt phẳng đi qua trọng tâm tam giác $\Large SAB$ và song song với mặt đáy $\Large (ABCD)$ chia khối chóp $\Large S.ABCD$ thành hai phần. Tính thể tích V của phần chứa điểm $\Large S$.

• A.

  A. $\Large V=8$

• B.

  B. $\Large V=24$

• C.

  C. $\Large V=36$

• D.

  D. $\Large V=12$

Chọn D

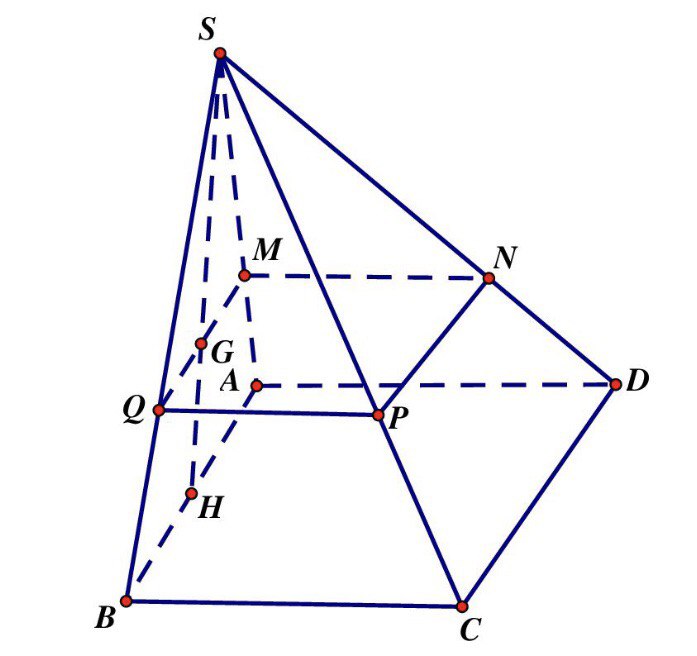
Gọi $\large H$ là trung điểm $\large AB$. Do $\Large \Delta SAB$ đều nên $\Large SH \bot \left( {ABCD} \right)$

Gọi độ dài cạnh đáy là x, ta có:

$\Large {S_{SAB}} = \dfrac{{{x^2}\sqrt 3 }}{4} = \dfrac{{27\sqrt 3 }}{4} \Leftrightarrow x = 3\sqrt 3 $.

Vậy $\Large SH = \dfrac{{x\sqrt 3 }}{2} = \dfrac{{3\sqrt 3 .\sqrt 3 }}{2} = \dfrac{9}{2}$

Suy ra $\Large {S_{S.ABCD}} = \dfrac{1}{3}.SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{9}{2}.{\left( {3\sqrt 3 } \right)^2} = \dfrac{{81}}{2}$ 

Dễ thấy mặt phẳng đi qua $\large G$ song song với mặt đáy cắt chóp là hình vuông $\large MNPQ$ như hình vẽ.

Ta có $\Large \dfrac{{MQ}}{{AB}} = \dfrac{{SG}}{{SH}} = \dfrac{2}{3}$ nên $\Large MQ = \dfrac{2}{3}AB = 2\sqrt 3$ và $\Large SG = \dfrac{2}{3}SH = 3$.

Vậy $\Large V = \dfrac{1}{3}SG.{S_{MNPQ}} = \dfrac{1}{3}.3.{\left( {2\sqrt 3 } \right)^2} = 12$