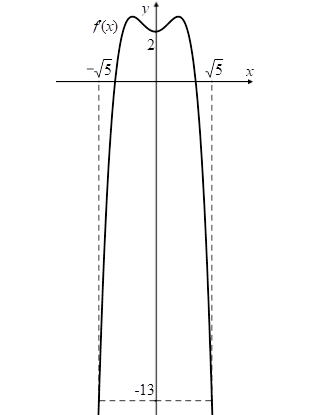
Cho hàm số $\Large y = f(x)$ có đồ thị $\Large y = f{}'(x)$ như hình v

Cho hàm số $\Large y = f(x)$ có đồ thị $\Large y = f{}'(x)$ như hình vẽ. Xét hàm số $\Large g(x) = 2f(x) + 2x^{3} - 4x - 3m - 6\sqrt{5}$ với $\Large m$ là số thực. Để $\Large g(x) \leq 0,$ $\Large \forall x \in \left [ -\sqrt{5}; \sqrt{5} \right ]$ thì điều kiện của $\Large m$ là

• A.

  A. $\Large m \geq \dfrac{2}{3}f\left ( -\sqrt{5} \right ) - 4\sqrt{5}.$

• B.

  B. $\Large m \leq  \dfrac{2}{3}f\left ( \sqrt{5} \right ).$

• C.

  C. $\Large m \leq \dfrac{2}{3}f\left ( 0\right ) - 2\sqrt{5}.$

• D.

  D. $\Large m \geq  \dfrac{2}{3}f\left ( \sqrt{5} \right ).$

Chọn D

Ta có:

$\Large g(x)\leq 0 \Leftrightarrow 2f(x) + 2x^{3} - 4x \leq 3m + 6\sqrt{5}.$

Đặt $\Large h(x) = 2f(x) + 2x^{3} - 4x$ thì bất phương trình $\Large g(x) \leq 0 \Leftrightarrow h(x) \leq 3m + 6\sqrt{5}.$

$\Large h{}'(x) = 2f{}'(x) + 2.3x^{2} - 4 = 2\left ( f{}'(x) - (-3x^{2} + 2) \right ).$

Vẽ đồ thị hàm số $\Large y = -3x^{2} + 2$ trên cùng hệ trục tọa độ với hàm số $\Large y = f{}'(x)$.

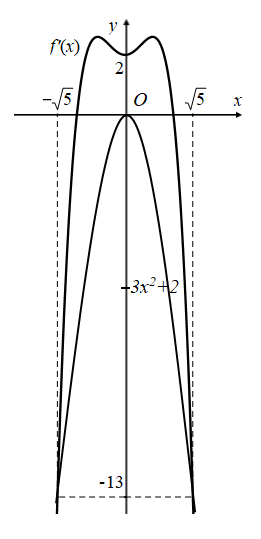
Ta thấy:

$\Large f{}'(x) \geq -3x^{2} + 2 \forall x \in \left [ -\sqrt{5}; \sqrt{5} \right ]$ nên $\Large  h{}'(x) \geq 0, x \in \left [ -\sqrt{5}; \sqrt{5} \right ]$.

Suy ra: $\Large h(x) \leq h(\sqrt{5}), x \in \left [ -\sqrt{5}; \sqrt{5} \right ]$

hay $\Large \max_{\left [ -\sqrt{5};\sqrt{5} \right ]}h(x) = h(\sqrt{5}) = 2f(\sqrt{5}) + 6\sqrt{5}.$

Do đó: $\Large h(x) \leq 3m + 6\sqrt{5}, x \in \left [ -\sqrt{5}; \sqrt{5} \right ]$ $\Large \Leftrightarrow \max_{\left [ -\sqrt{5}; \sqrt{5} \right ]}h(x) \leq 3m + 6\sqrt{5}$ $\Large =2f\left(\sqrt{5}\right)+6\sqrt{5}\le 3m+6\sqrt{5}$ $\Large \Leftrightarrow m \geq \dfrac{2}{3}f\left ( \sqrt{5} \right ).$