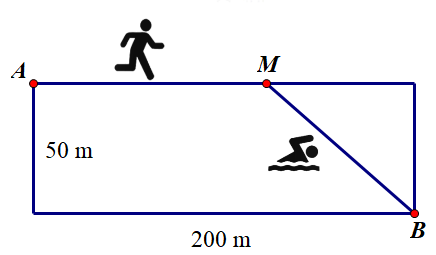
Có một cái hồ hình chữ nhật rộng 50m, dài 200m. Một vận động viên tập

Có một cái hồ hình chữ nhật rộng 50m, dài 200m. Một vận động viên tập luyện chạy phối hợp với bơi như sau: Xuất phát từ vị trí điểm A chạy theo chiều dài bể bơi đến vị trí điểm M và bơi từ vị trí điểm M thẳng đến đích là điểm B (đường nét đậm) như hình vẽ. Hỏi vận động viên đó nên chọn vị trí điểm M cách điểm A bao nhiêu mét (kết quả làm tròn đến hàng đơn vị) để đến đích nhanh nhất, biết rằng vận tốc bơi là 1,6 m/s, vận tốc chạy là 4,8 m/s.

 

• A.

  A. 178m

• B.

  B. 182m

• C.

  C. 180m

• D.

  D. 184m

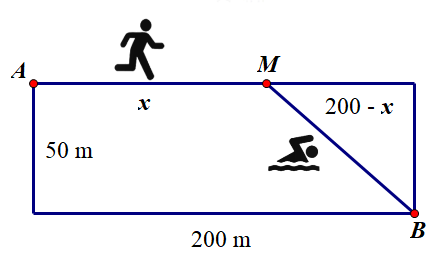
Đặt $\Large AM=x (m)(0

Thời gian vận động viên chạy từ A đến M: $\Large t_1=\dfrac{x}{4,8}(s)$

Thời gian vận động viên bơi từ M đến B: $\Large t_2=\dfrac{\sqrt{(200-x)^2+50^2}}{1,6}(s)$

Thời gian vận động viên chạy phối hợp với bơi từ A đến M:

$\large t=t_1+t_2=\dfrac{x}{4,8}+\dfrac{\sqrt{(200-x)^{2}+50^{2}}}{1,6}$

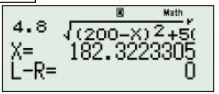
Ta có $\large t^{\prime}=\dfrac{1}{4,8}+\dfrac{-(200-x)}{1,6 \cdot \sqrt{(200-x)^{2}+50^{2}}}=0\Leftrightarrow \dfrac{1}{4,8}=\dfrac{200-x}{1,6\sqrt{(200-x)^2+50^2}}\Leftrightarrow \left[\begin{matrix}200-x=\dfrac{25}{\sqrt{2}}\\ 200-x=-\dfrac{25}{\sqrt{2}}\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}x\simeq 182\\ x\simeq 218 (ktm)\end{matrix}\right. \Leftrightarrow x=182 m$

Lập bảng biến thiên ta thấy để vận động viên về đích nhanh nhất $\Large (t_{min})$ suy ra vận động viên đó nên chọn điểm M cách điểm A 182 m.

Trắc nghiệm : Giải phương trình t'=0 bằng cách bấm máy, sử dụng SHIFT CALC: