Tìm m để phương trình $\large \left|x^{4}-5 x^{2}+4\right|=\log _{2} m

Tìm m để phương trình $\large \left|x^{4}-5 x^{2}+4\right|=\log _{2} m$ có 8 nghiệm thực phân biệt:

 

• A.

  A. $\large 0

• B.

  B. $\large -\sqrt[4]{2^{9}}

• C.

  C. Không có giá trị của m

• D.

  D. $\large 1

ĐK: m>0

Số nghiệm của phương trình $\large \left|x^{4}-5 x^{2}+4\right|=\log _{2} m$ là số giao điểm của đồ thị hàm số $\large y=\left|x^{4}-5 x^{2}+4\right|$ là đường thẳng $\large y=\log _{2} m$

Xét hàm số $\large f(x)=x^{4}-5 x^{2}+4$ có TXĐ: D=R.

$\large y^{\prime}=4 x^{3}-10 x=0 \Leftrightarrow\left[\begin{array}{r}
x=0 \Rightarrow y=4 \\
x=\pm \dfrac{\sqrt{10}}{2} \Rightarrow y=-\frac{9}{4}
\end{array}\right.$

BBT:

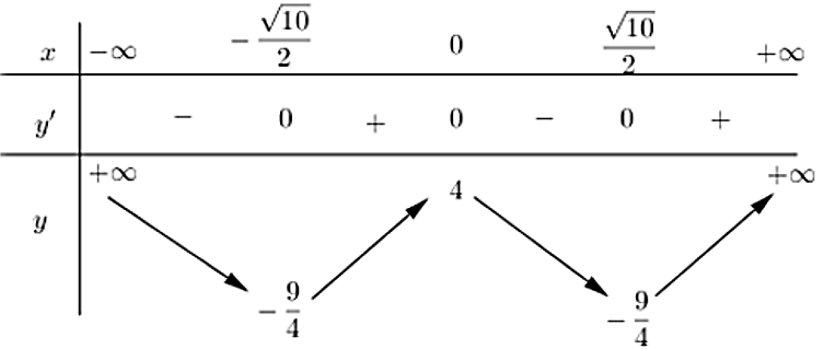
Từ đó ta suy ra được BBT của đồ thị hàm số $\large y=\left|x^{4}-5 x^{2}+4\right|$ như sau:

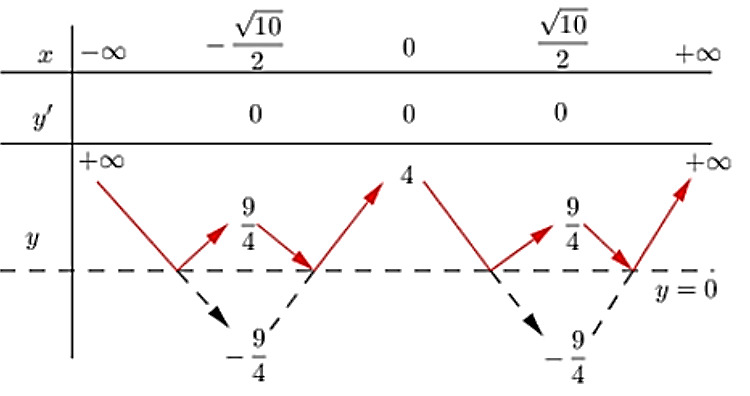
Do đó để phương trình $\large \left|x^{4}-5 x^{2}+4\right|=\log _{2} m$ có 8 nghiệm thực phân biệt thì đường thẳng $\large y=\log _{2} m$ cắt đồ thị hàm số $\large y=\left|x^{4}-5 x^{2}+4\right|$ tại 8 điểm phân biệt.

Dựa vào bảng biến thiên suy ra $\large 0<\log _{2} m<\dfrac{9}{4} \Leftrightarrow 1

Chọn D.