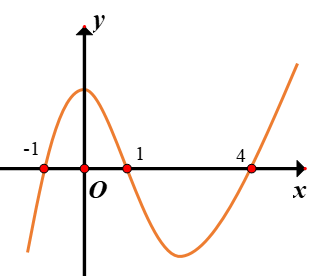
Cho hàm số $\large f(x)=x^{2}-4 x^{2}-x+4$ có đồ thị như hình vẽ. Có b

Cho hàm số $\large f(x)=x^{2}-4 x^{2}-x+4$ có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình sau có 4 nghiệm thuộc đoạn [0;2]

$\large 2019 f\left(\sqrt{15 x^{2}-30 x+16}\right)-m \sqrt{15 x^{2}-30 x+16}-m=0$

• A.

  A. 4541

• B.

  B. 4542

• C.

  C. 4543

• D.

  C. 4540

Chọn đáp án B

Theo đề $\large f^{\prime}(x)\simeq (x+1)(x-1)(x-4)$

$\large \forall x \in[0 ; 2]: t=\sqrt{15 x^{2}-30 x+16}=\sqrt{15(x-1)^{2}+1} \geq 1 ; t(0)=t(2)=4 \Rightarrow t \in[1 ; 4]$

Với t>1 thì phương trình có 2 nghiệm x thỏa mãn.

Với t=1 có 1 nghiệm x thỏa mãn.

$\large \mathrm{BPT} \Leftrightarrow 2019 f(t)=m(t+1) \Leftrightarrow 2019(t+1)(t-1)(t-4)=m(t+1)$

Xét $\large t \in(1 ; 4]$

$\large \Rightarrow m=g(t)=2019(t-1)(t-4)=2019\left(t^{2}-5 t+4\right)=2019\left[\left(t-\frac{5}{2}\right)^{2}-\frac{9}{4}\right] \geq2019\left(-\frac{9}{4}\right)=-4542,75$

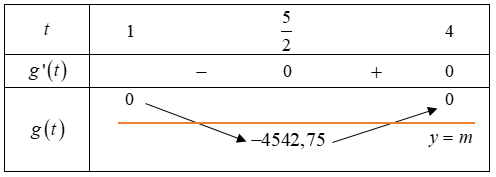
Yêu cầu bài toán $\large \Leftrightarrow-4542,75