Cho hàm bậc bốn $y=f\left( x \right)$ có đồ thị là đường cong trong hì

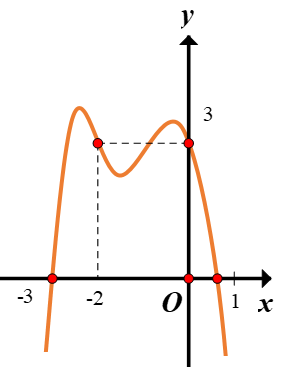
Cho hàm bậc bốn $y=f\left( x \right)$ có đồ thị là đường cong trong hình vẽ. Số nghiệm thực phân biệt của phương trình $f\left( {{\left( x+2 \right)}^{2}}f\left( x \right) \right)-3=0$ là:

 

• A. A. 8
• B. B. 6
• C. C. 9
• D. D. 12

$f\left( {{\left( x+2 \right)}^{2}}f\left( x \right) \right)-3=0\Leftrightarrow f\left( {{\left( x+2 \right)}^{2}}f\left( x \right) \right)=3\left( * \right)$
Ta có 
$f\left( {{\left( x+2 \right)}^{2}}f\left( x \right) \right)=3$$\Rightarrow \left[ \begin{matrix}
   {{\left( x+2 \right)}^{2}}f\left( x \right)=0  \\
   {{\left( x+2 \right)}^{2}}f\left( x \right)=a\in \left( -1;0 \right)  \\
   {{\left( x+2 \right)}^{2}}f\left( x \right)=b=-2  \\
   {{\left( x+2 \right)}^{2}}f\left( x \right)=c\in \left( -3;-2 \right)  \\
\end{matrix} \right.$
Xét phương trình ${{\left( x+2 \right)}^{2}}f\left( x \right)=0\Leftrightarrow \left[ \begin{matrix}
  & x=-2 \\ 
 & f\left( x \right)=0 \\ 
\end{matrix} \right.$ mà $f\left( x \right)=0$ có hai nghiệm $\Rightarrow \text{phương trình} {{\left( x+2 \right)}^{2}}f\left( x \right)=0$ có ba nghiệm
Xét phương trình ${{\left( x+2 \right)}^{2}}f\left( x \right)=a<0$
Do ${{\left( x+2 \right)}^{2}}\ge 0;x=-2$ không là nghiệm của phương trình $\Rightarrow f\left( x \right)=\frac{a}{{{\left( x+2 \right)}^{2}}}<0$
Xét $g\left( x \right)=\frac{a}{{{\left( x+2 \right)}^{2}}}\Rightarrow g'\left( x \right)=\frac{-2a}{{{\left( x+2 \right)}^{3}}}$
Bảng biến thiên:

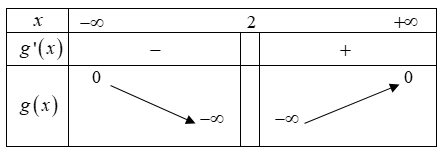
Từ bảng biến thiên với $f\left( x \right)<0\Rightarrow f\left( x \right)=\frac{a}{{{\left( x+2 \right)}^{2}}}$ có 2 nghiệm
Tương tự ${{\left( x+2 \right)}^{2}}f\left( x \right)=b$ và ${{\left( x+2 \right)}^{2}}f\left( x \right)=c\left( b,c<0 \right)$ mỗi phương trình cũng có hai nghiệm.
Vậy số nghiệm của phương trình $f\left( {{\left( x+2 \right)}^{2}}f\left( x \right) \right)=3$ là 9 nghiệm