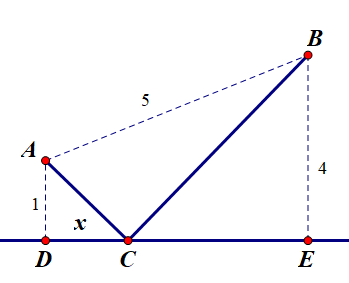
Có hai cây cột dựng trên mặt đất lần lượt cao 1m và 4m, đỉnh của hai c

Có hai cây cột dựng trên mặt đất lần lượt cao 1m và 4m, đỉnh của hai cây cột cách nhau 5m. 

Người ta chọn một vị trí trên mặt đất (nằm giữa chân cột) để giăng dây nối đến hai đỉnh cột để trang trí như hình vẽ dưới. Tính độ dài dây ngắn nhất.

• A.

  A. $\large \sqrt{41}$

• B.

  B. $\large \sqrt{37}$

• C.

  C. $\large \sqrt{29}$

• D.

  D. $\large 3 \sqrt{5}$

Đặt CD=x, x>0. Ta tính được $\large D E=\sqrt{5^{2}-(4-1)^{2}}=4$

Ta có $\large A C+B C=\sqrt{x^{2}+1}+\sqrt{(4-x)^{2}+16}=f(x)$

Khi đó: $\large f^{\prime}(x)=\dfrac{x}{\sqrt{x^{2}+1}}+\dfrac{x-4}{\sqrt{x^{2}-8 x+32}}$

Giải phương trình $\large f^{\prime}(x)=0 \Leftrightarrow x\sqrt{x^2-8x+32}=(4-x)\sqrt{x^2+1} (x<4)\Leftrightarrow 15x^2+8x-16=0\Leftrightarrow\left[\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{3} \end{matrix}\right.$

Vậy  $\large x=\dfrac{4}{5} (tm)$ và tìm được $\large \min f(x)=\sqrt{41}$.

Đáp án đúng: A