Có bao nhiêu số nguyên m để hàm số $\large f(x)=x^4-2(m^2-3m)x^2+3$ đồ

Có bao nhiêu số nguyên m để hàm số $\large f(x)=x^4-2(m^2-3m)x^2+3$ đồng biến trên khoảng $\large (2; +\infty)$

• A. 4
• B. 6
• C. 2
• D. 5

Ta có: 

-TXĐ : $\large  D = R$

- $\large f'(x)=4x^3-4(m^2-3m)x=4x[x^2-(m^2-3m)]$

Yêu cầu bài toán tương đương với:  

$\large f'(x)=4x^3-4(m^2-3m)x=4x[x^2-(m^2-3m)]\geq 0, \forall x\in (2; +\infty)$

Khi đó ta có các trường hợp sau.
Trường hợp 1: $\large m^2-3m\leq 0\Leftrightarrow m\in [0; 3]$  

Do $\large m\in\mathbb{Z}\Rightarrow m\in\left\{0; 1; 2; 3\right\}$

$\large f'(x)=4x[x^2-(m^2-3m)]\geq 0, \forall x\in (2; +\infty)\Rightarrow m\in \left\{0; 1; 2; 3\right\} $ thỏa mãn bài toán .

Trường hợp 2: $\large m^2-3m>0$

$\large \Rightarrow f'(x)=4x(x+\sqrt{m^2-3m})(x-\sqrt{m^2-3m})$

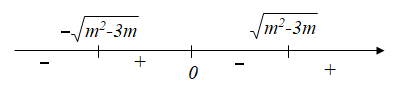
Để thỏa mãn trong trường hợp này $\large \Leftrightarrow \left\{\begin{align}& m^2-3m>0\\& \sqrt{m^2-3m}\leq 2\\\end{align}\right.$ $\large \Leftrightarrow \left\{\begin{align}& m\in (-\infty; 0)\cup (3; +\infty)\\& m\in [-1; 4]\\\end{align}\right.$

Do $\large m\in\mathbb{Z}\Rightarrow m\in \left\{-1; 4\right\}$  

Từ hai trường hợp trên ta có : $\large m\in{-1;0;1;2;3;4}$