Cho tứ diện ABCD có AB $\large =a\sqrt{6}$, tam giác ACD đều, hình chi

Cho tứ diện ABCD có AB $\large =a\sqrt{6}$, tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD) trùng với trực tâm H của tam giác BCD , mặt phẳng (ADH) tạo với mặt phẳng (ACD) một góc $\large 45^\circ$. Tính thể tích khối tứ diện ABCD.

• A. $\large \dfrac{3a^3}{2}$
• B. $\large \dfrac{9a^3}{4}$
• C. $\large \dfrac{27a^3}{4}$
• D. $\large \dfrac{3a^3}{4}$

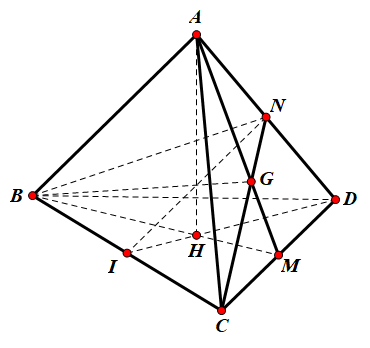
Gọi M là giao điểm của BH và CD

Ta có: $\large \left\{\begin{align}& CD\perp AH\\& CD\perp BH\\\end{align}\right.$ $\large \Rightarrow  CD\perp (ABH)\Rightarrow CD\perp AM$ 

Mà $\large \Delta ACD$  là tam giác đều $\large \Rightarrow M$ là trung điểm của CD

$\large \Rightarrow \Delta BCD$ cân tại $\large B\Rightarrow BC=BD$ (1)

Gọi N là trung điểm của $\large AD\Rightarrow CN\perp AD$ 

Lại có: $\large \left\{\begin{align}& BC\perp AH\\& BC \perp DH\\\end{align}\right.$  $\large \Rightarrow BC\perp (ADH)\Rightarrow BC\perp AD$ 

$\large AD\perp (BCN)\Rightarrow AD \perp BN\Rightarrow \Delta ABD$ cân tại B $\large \Rightarrow BA=BD$ (2)

từ (1) và (2) $\large \Rightarrow BA=BD=BC=a\sqrt{6}$

Gọi G là giao điểm của CN và AM

Ta có: $\large \left\{\begin{align}& BG\perp CD, (CD\perp (ABH))\\& BG\perp AD,( AD\perp (BCN))\\\end{align}\right.$ $\large \Rightarrow BG\perp (ACD)$ 

Gọi I là giao điểm của DH và BC

Khi đó: $\large \widehat{(ACD); (ADH)}=\widehat{INC}=45^\circ\Rightarrow \widehat{ICN}=45^\circ\Rightarrow \Delta BGC$ vuông cân tại G

$\large \Rightarrow BG=CG=\dfrac{BC}{\sqrt{2}}=\dfrac{a\sqrt{6}}{\sqrt{2}}=a\sqrt{3}$ 

Mặt khác: $\large CG=\dfrac{2}{3}.CN=\dfrac{2}{3}.AC.\dfrac{\sqrt{3}}{2}\Rightarrow AC=CG.\sqrt{3}=3a$ 

$\large S_{ACD}=(3a)^2.\dfrac{\sqrt{3}}{4}=\dfrac{9a^2\sqrt{3}}{4}$  

$\large V_{ABCD}=\dfrac{1}{3}.BG.S_{\Delta ACD}=\dfrac{1}{3}.a\sqrt{3}.\dfrac{9a^2\sqrt{3}}{4}=\dfrac{9a^3}{4}$