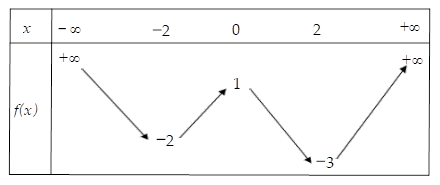
Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình bên

Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình bên. Xác định số nghiệm của phương trình $\large \left|f(x^3-3x^2)\right|=\dfrac{3}{2}$, biết $\large f(-4)=0$

• A. 9
• B. 6
• C. 7
• D. 10

Đặt $\large g(x)=x^3-3x^2$. Ta có: $\large g'(x)=3x^2-6x=0$ $\large \Leftrightarrow \left[\begin{align}& x=2\Rightarrow y=-4\\& x=0\Rightarrow y=0\\\end{align}\right.$

Theo đề bài ta có bảng biến thiên:

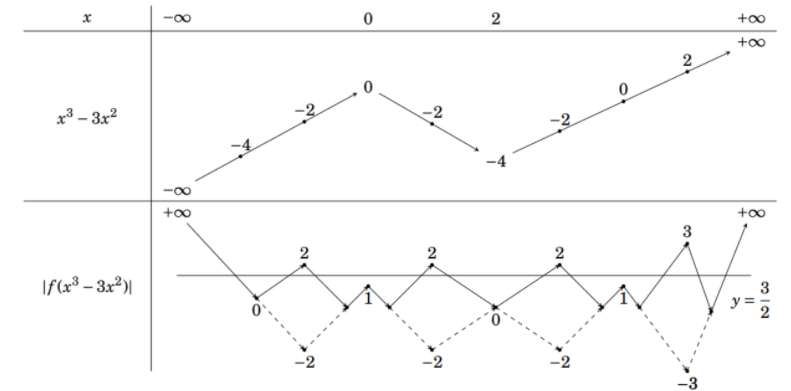
Số nghiệm của phương trình $\large \left| f(x^3-3x^2)\right|=\dfrac{3}{2}$ bằng số giao điểm của đồ thị hàm số $\large \left| f(x^3-3x^2)\right|$ và đường thẳng $\large y=\dfrac{3}{2}$

Dựa vào bảng biến thiên ta thấy phương trình đã cho có 10 nghiệm.