Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số $\lar

Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số $\large y = x^4-4x^2+ m-2$ cắt trục hoành tại bốn điểm phân biệt

• A. 3
• B. 4
• C. 2
• D. Vô số

Chọn A

Phương trình hoành độ giao điểm: $\large x^4-4x^2+m-2= 0\Leftrightarrow x^4-4x^2-2=-m$

Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số $\large y = x^4-4x^2-2$ và đường thẳng $\large y = -m$

Xét hàm số: $\large y = x^4-4x^2-2$; $\large y'=4x^3-8x;\, y'=0\Leftrightarrow$ $\large \left[\begin{align}& x=0\\& x= \pm \sqrt{2}\\\end{align}\right. $

Bảng biến thiên 

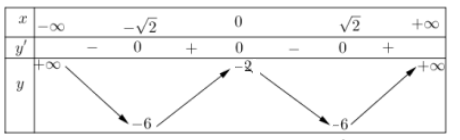
Từ bảng biến thiên suy ra: phương trình có bốn nghiệm phân biệt khi $\large -6< -m< -2\Leftrightarrow 6> m> 2$

Vậy có 3 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán