Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. $\lar

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. $\large AD= 2,\, BA= BC= 1$. Cạnh bên SA vuông góc với đáy  và $\large SA= \sqrt{2}$. Gọi H là hình chiếu vuông góc của A trên SB. Tính thể tích V của khối đa diện SAHCD

• A. $\large V=\dfrac{4\sqrt{2}}{9}$
• B. $\large V= \dfrac{2\sqrt{2}}{3}$
• C. $\large V= \dfrac{4\sqrt{2}}{3}$
• D. $\large V= \dfrac{2\sqrt{2}}{9}$

Chọn A

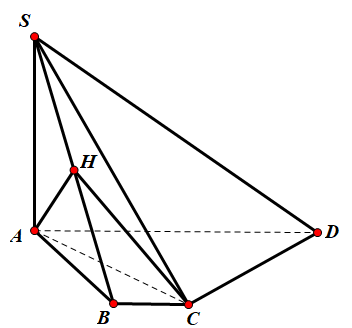
$\large V_{SAHCD}= V_{S.ABCD}- V_{H.ABC} $

$\large V_{S.ABCD} = \dfrac{1}{3}.SA.S_{ABCD} = \dfrac{1}{3}\sqrt{2}.\dfrac{1}{2}(1+2).1= \dfrac{\sqrt{2}}{2}$

Tam giác BHA đồng dạng với tam giác BAS

Suy ra: $\large \dfrac{BH}{BA} = \dfrac{BA}{BS}\Leftrightarrow BH = \dfrac{1}{\sqrt{3}}$

$\large AH= \sqrt{1-\dfrac{1}{3}}= \sqrt{\dfrac{2}{3}}$

$\large V_{C.ABH} = \dfrac{1}{3}.BC.S_{ABH}= \dfrac{1}{3}.1.\dfrac{1}{2}.\dfrac{1}{\sqrt{3}}.\sqrt{\dfrac{2}{3}}= \dfrac{\sqrt{2}}{18}$

$\large V_{SAHCD} = \dfrac{\sqrt{2}}{2} - \dfrac{\sqrt{2}}{18}= \dfrac{4\sqrt{2}}{9}$