Cho hình trụ hai đáy là hai hình tròn (O) và (O'), chiều cao có độ dài

Cho hình trụ hai đáy là hai hình tròn (O) và (O'), chiều cao có độ dài bằng 2a. Gọi $\large (\alpha)$ là mặt phẳng đi qua trung điểm OO' và tạo với OO' một góc $\large 30^\circ$. Biết $\large (\alpha)$ cắt đường tròn đáy theo một dây cung có độ dài $\large a\sqrt{6}$. Thể tích khối trụ là

• A.

  $\large \dfrac{11\pi a^3}{3}$

• B.

  $\large \dfrac{11\pi a^3}{6}$

• C.

  $\large \dfrac{2\pi a^3}{3}$

• D.

  $\large 2\pi a^3$

Chọn A

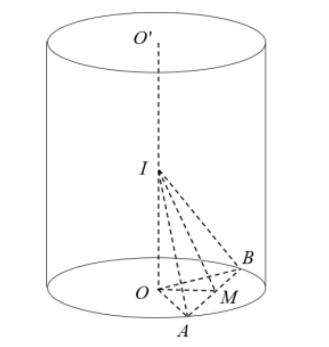
Gọi I là trung điểm của OO', suy ra: $\large OI= a$

Mặt phẳng $\large (\alpha)$ cắt đường tròn (O) tại hai điểm A và B, suy ra: $\large AB= a\sqrt{6}$

Gọi M là trung điểm của đoạn thẳng AB, suy ra: $\large AM= \dfrac{a\sqrt{6}}{2}$

Ta có: $\large \left\{\begin{align}& AB\perp OM\\& AB\perp OI\\\end{align}\right. $ $\large \Rightarrow AB\perp (OMI)\Rightarrow (IAB)\perp (OMI)$

Do đó góc $\large \widehat{OIM}$ chính là góc giữa hai mặt phẳng $\large (\alpha)$ và OO', suy ra: $\large \widehat{OIM}= 30^\circ$

Xét tam giác IOM vuông tại O, ta có: $\large OM=OI.\tan\widehat{OIM} = a.\tan 30^\circ= \dfrac{a\sqrt{3}}{3}$

Xét tam giác OMA vuông tại M, ta có: $\large OA= \sqrt{OM^2+ MA^2} = \sqrt{\left(\dfrac{a\sqrt{3}}{3}\right)^2 + \left(\dfrac{a\sqrt{6}}{2}\right)^2}= \dfrac{a\sqrt{66}}{6}$

Thể tích khối trụ là: $\large V= OO'.\pi.OA^2= 2a\pi.\left(\dfrac{a\sqrt{66}}{6}\right)^2= \dfrac{11\pi a^3}{3}$