Cho phương trình $\large 7^x+ m = \log_7(x-m)$ với m là tham số. Có ba

Cho phương trình $\large 7^x+ m = \log_7(x-m)$  với m là tham số. Có bao nhiêu giá trị nguyên của $\large m\in (-25; 25)$ để phương trình đã cho có nghiệm?

• A. 24
• B. 25
• C. 9
• D. 26

Chọn A

Ta có: $\large 7^x + m = \log_7 (x-m) \Leftrightarrow 7^x+ x= x-m + \log_7 (x-m)\Leftrightarrow  7^x+x = 7^{\log_7 (x-m)}+\log_7 (x-m)$ (*)

Xét hàm số $\large f(t) = 7^t+ t$ với $\large t\in \mathbb{R}$, có $\large f(t) = 7^t.\ln 7+ 1> 0,\forall t\in \mathbb{R}$

Suy ra hàm số $\large y = f(t)$ đồng biến trên $\large \mathbb{R}$

Ta có: $\large (*)\Leftrightarrow f(x) = f\left(\log_7 (x-m) \right)\Leftrightarrow x= \log_7 (x-m) \Leftrightarrow x-m = 7^x\Leftrightarrow m = x-7^x$

Xét hàm số $\large g(x) = x-7^x\Rightarrow g'(x) = 1-7^x\Rightarrow g'(x) = 0\Leftrightarrow x= \log_7\left( \dfrac{1}{\ln 7}\right)$

Bảng biến thiên

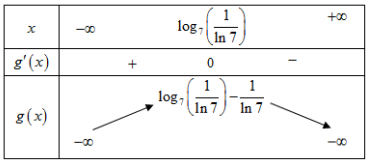
Từ bảng biến thiên suy ra phương trình có nghiệm khi và chỉ khi $\large m\leq \log_7\left(\dfrac{1}{\ln 7}\right) - \dfrac{1}{\ln 7} \approx -0,86$ 

mà $\large m\in (-25; 25),\, m\in \mathbb{Z}$ nên $\large m\in \left\{-24; -23; ...; -1\right\}$

Vậy có 24 giá trị nguyên của tham số $\large m\in (-25; 25)$ thỏa mãn phương trình có nghiệm