Cho hình chóp S.ABC có $\large SA= SB = SC =a,\, \widehat{ASB} = 60^\c

Cho hình chóp S.ABC có $\large SA= SB = SC =a,\, \widehat{ASB} = 60^\circ,\ ,\widehat{BSC} = 90^\circ$ và $\large \widehat{CSA}= 120^\circ$. Khoảng cách giữa hai đường thẳng AC và SB là: 

• A. A. $\large \dfrac{a\sqrt{22}}{11}$
• B. B. $\large \dfrac{a\sqrt{3}}{3}$
• C. C. $\large \dfrac{a\sqrt{3}}{4}$
• D. D. $\large \dfrac{a\sqrt{22}}{22}$

Chọn A

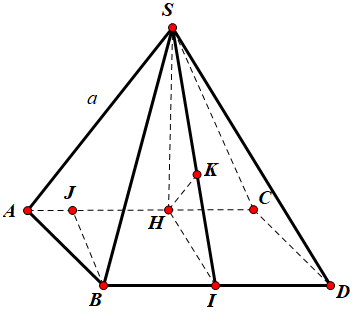
Xét tam giác SAC có: 

$\large AC^2= SA^2+SC^2-2SA.SC.\cos 120^\circ= a^2+a^2-2a.a.\left(-\dfrac{1}{2}\right)=3a^2\Rightarrow AC= a\sqrt{3}$

Xét tam giác ABC có: $\large AB=a, BC= a\sqrt{2},AC= a\sqrt{3}\Rightarrow AB^2+ BC^2= AC^2\Rightarrow \Delta ABC$ vuông tại B

Gọi BJ là đường cao của tam giác ABC $\large \Rightarrow BJ= \dfrac{AB.BC}{AC} = \dfrac{a.a\sqrt{2}}{a\sqrt{3}}= \dfrac{a\sqrt{6}}{3}$

Gọi H là hình chiếu của S lên (ABC), do $\large SA= SB= SC=a $ nên H là tâm đường tròn ngoại tiếp $\large \Delta ABC$ mà $\large \Delta ABC$ vuông tại B $\large \Rightarrow $ H là trung điểm AC

Dựng hình bình hàng ABCD, khi đó: $\large d(AC, SB) = d(AC, (SBD))= d(H, (SBD))$

Gọi I là hình chiếu của H lên BD, ta có: $\large \left\{\begin{align}& BD\perp SH\\& BD\perp HI\\\end{align}\right.$ $\large \Rightarrow BD\perp (SHI)$

Gọi K là hình chiếu của H lên SI, ta có: $\large \left\{\begin{align}& HK\perp SI\\& HK\perp BD\\\end{align}\right. $ $\large \Rightarrow HK\perp (SBD) \Rightarrow d(H, (SBD))= HK$

Xét $\large \Delta SHI$ ta có: $\large HK = \dfrac{SH.HI}{SI}= \dfrac{SH.BJ}{SI}= \dfrac{\dfrac{a}{2}.\dfrac{a\sqrt{6}}{3}}{\sqrt{\left(\dfrac{a}{2} \right )^2+ \left(\dfrac{a\sqrt{6}}{3}\right)^2}}=\dfrac{a\sqrt{22}}{11}$