Cho tứ diện ABCD có $\large AD\perp (ABC) $, tam giác ABC vuông tại B

Cho tứ diện ABCD có $\large AD\perp (ABC) $, tam giác ABC vuông tại B . Biết $\large BC= a,\, AB= a\sqrt{3},\, AD= 3a$ Quay các miền tam giác ABC và ABD xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay đó bằng

• A. $\large \dfrac{4\pi a^3\sqrt{3}}{16}$
• B. $\large \dfrac{3\pi a^3\sqrt{3}}{16}$
• C. $\large \dfrac{8\pi a^3\sqrt{3}}{16}$
• D. \large \dfrac{5\pi a^3\sqrt{3}}{16}$

Chọn B

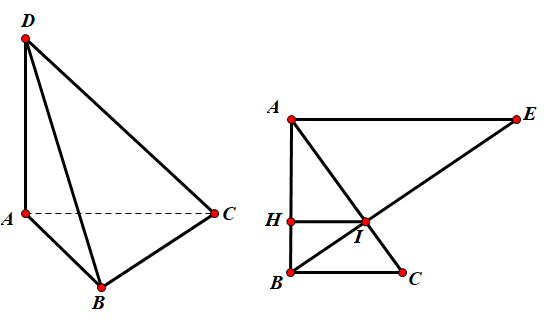
Trong ( ABC) lấy điểm E sao cho $\large AE= 3a,\, AE\perp AB$

Khi đó khối tròn xoay khi quay miền tam giác ABD quanh đường thẳng AB cũng chính là khối tròn xoay khi quay miền tam giác ABE quanh đường thẳng AB .
Gọi I là giao điểm của BD và AC .
Khi đó, phần chung của hai khối tròn xoay đã cho chính là khối tròn xoay tạo thành khi quay miền tam giác ABI quanh trục AB .
Kẻ IH vuông góc với AB tại H .
Suy ra thể tích phần chung của hai khối tròn xoay đã cho là $\large V= \dfrac{1}{3}.\pi.IH^2.AB$

Ta có: $\large BC//AE\Rightarrow \dfrac{IC}{IA} = \dfrac{BC}{AE}  =\dfrac{1}{3}$

$\large IH//BC\Rightarrow \dfrac{HI}{BC} = \dfrac{AI}{IC} = \dfrac{3}{4}\Rightarrow HI = \dfrac{3a}{4}$

Vậy $\large V= \dfrac{1}{3}\pi.\left(\dfrac{3a}{4}\right)^2.a\sqrt{3}= \dfrac{3\pi a^3\sqrt{3}}{16}$