Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m sao cho bất phương

Có bao nhiêu giá trị nguyên bé hơn 10 của tham số m  sao cho bất phương trình $\Large \log_{2}^2x-1+2\sqrt{\log_{2}^2x+1}-m\leq0$ thõa mãn với mọi $\Large x \in \left[1; 2^{\sqrt{3}}\right]$ ?

• A.

  A. 3

• B.

  B. 4

• C.

  C. 5

• D.

  D.6

Chọn B

Điều kiện: x > 0

$\Large \log_{2}^2x-1+2\sqrt{\log_{2}^2x+1}-m\leq0$$\Large  \Leftrightarrow \log_{2}^2x+1+2\sqrt{\log_{2}^2x+1}-2\leq m$ (1)

Đặt $\Large t=\sqrt{\log_{2}^2x+1}$ với $\Large x\in\left[1; 2^{\sqrt{3}}\right]\Rightarrow t\in [1; 2]$

Khi đó $\Large (1)\Leftrightarrow t^2+2t-2\leq m$

Xét hàm số: $\Large f(t)=t^2+2t-2$ trên $\Large [1; 2]; f'(t)=2t+2=0\Rightarrow t=-1$

Bảng biến thiên 

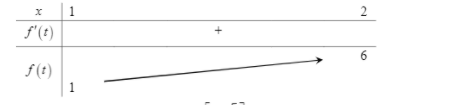
Bất phương trình thỏa mãn với mọi x thuộc $\Large \left[1; 2^{\sqrt{3}}\right]$ khi $\Large m\geq6$