Cho tứ diện $\Large ABCD$, $\Large M$ là một điểm nằm trong tứ diện, b

Cho tứ diện $\Large ABCD$, $\Large M$ là một điểm nằm trong tứ diện, bốn mặt phẳng chứa $\Large M$ lần lượt song song với các mặt $\Large (BCD)$, $\Large (CDA)$, $\Large (DAB)$, $\Large (ABC)$ chia khối tứ diện $\Large ABCD$ thành các khối đa diện trong đó có bốn khối tứ diện có thể tích lần lượt là 1;1;1;8. Thể tích của khối tứ diện $\Large ABCD$ bằng

• A. 121.
• B. 64.
• C. 125.
• D. 100.

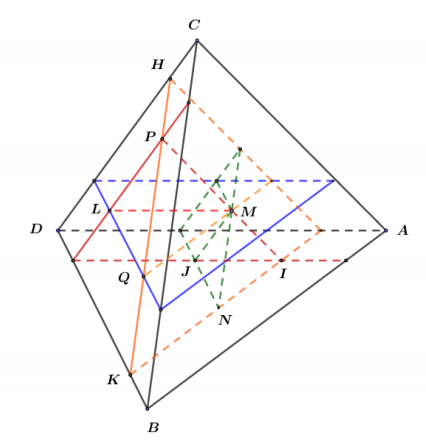
Do các mặt phẳng qua $\Large M$ và lần lượt song song với các mặt của tứ diện nên các cạnh của các tứ diện thu được có độ dài tương ứng tỉ lệ với độ dài các cạnh của tứ diện $\Large ABCD$.

Không mất tính tổng quát giả sử khối tứ diện $\Large MIJN$, $\Large MPLQ$ có thể tích lần lượt là 1 và 8.

Ta có $\Large \dfrac{V_{MIJN}}{V_{MPLQ}}=\dfrac{1}{8}$ nên $\Large \dfrac{MN}{PQ}=\dfrac{1}{2}$. Do $\Large MN=QK$ nên $\Large \dfrac{PQ}{QK}=\dfrac{2}{3}$ (1).

Vì hai khối tứ diện còn lại cũng có thể tích bằng 1 nên hoàn toàn tương tự ta có: $\Large \dfrac{PQ}{QH}=\dfrac{2}{3}$ (2).

Từ (1), (2) suy ra: $\Large \dfrac{PQ}{BC}=\dfrac{2}{5}$ nên $\Large \dfrac{V_{MPLQ}}{V_{ABCD}}=\left(\dfrac{2}{5}\right)^3=\dfrac{8}{125}$ $\Large \Rightarrow V_{ABCD}=125$.

Vậy $\Large V_{ABCD}=125$.