Cho tứ diện $\large ABCD$ có $\large AB,AC$ và $\large AD$ đôi một vuô

Cho tứ diện $\large ABCD$ có $\large AB,AC$ và $\large  AD$ đôi một vuông góc. Các điểm $\large M,N,P$ lần lượt à trung điểm các đoạn thẳng $\large BC,CD,BD$ Biết rằng $\large AB=4a,AC=6a,AD=7a$. Thể tích khối tứ diện đã cho bằng:

• A.

  A. $\large 7a^{3}$

• B.

  B. $\large 14a^{3}$

• C.

  C. $\large 21a^{3}$

• D.

  D. $\large 28a^{3}$

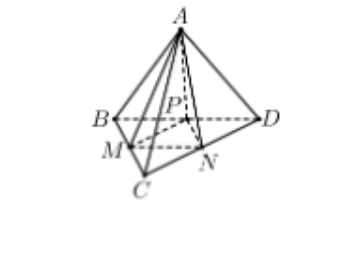
Tứ diện $\large ABCD$ có các cạnh $\large AB,AC,AD$ đôi một vuông góc nên $\large V_{ABCD}=\frac{1}{6}AB.AC.AD=28a^{3}$

Ta có $\large  S_{\bigtriangleup MNP}=\frac{1}{4}S_{\bigtriangleup BCD}\rightarrow V_{AMNP}=\frac{1}{4}V_{ABCD}=7a^{3}$

Đáp án A