Cho hình chóp tứ giác đều S.ABCD. Gọi N là trung điể

MỤC LỤC
Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD. Gọi N là trung điểm cạnh SB,M là điểm đối xứng với B qua A. Mặt phẳng (MNC) chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là V1,V2 với $\large V_{1}
Đáp án án đúng là: C
Lời giải chi tiết:
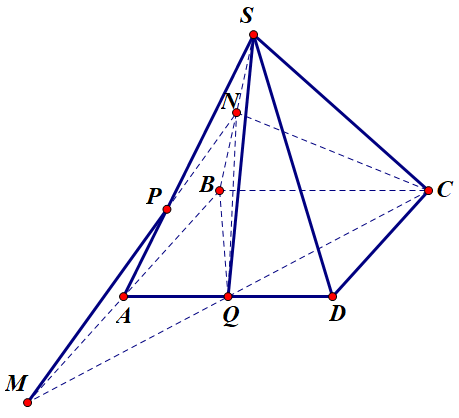
Gọi
P=MN∩SA,Q=MC∩AD . Ta có thiết diện của hình chóp cắt bởi mặt phẳng (MNC) là tứ giác CNPQ.
Dễ thấy P là trọng tâm của tam giác SBM và Q là trung điểm của đoạn AD.
Gọi V0 thể tích của phần chứa điểm S, P là diện tích của tứ giác ABCD và h chiều cao của hình chóp S.ABCD
Ta có V0=VS.NPQ+VS.NQC+VS.QDC
Mà VS.NPQ=SPSA.SNSB.VS.BAQ=23.12.13.SABQ.h=13.13.14.P.h=112V
VS.NQC=SNSB.VS.BQC=12.13.SBQC.h=12.13.12.P.h=14V
VS.QDC=13.SQDC.h=13.14.P.h=14V
Suy ra V0=V12+V4+V4=7V12
Dẫn đến V2=712V
Vậy V1=V−V2=512V
Đáp án C
Xem thêm các bài tiếp theo bên dưới