Cho hình lăng trụ $\large ABC.A'B'C'$ có $\large AA'=2a$, tam giác $\l

Cho hình lăng trụ $\large ABC.A'B'C'$ có $\large AA'=2a$, tam giác $\large ABC$ vuông tại $\large C$ và $\large\widehat{BAC}=60^{\circ}$, góc giữa cạnh bên $\large BB'$ và mặt phẳng đáy $\large (ABC)$ bằng $\large 60^{\circ}$. Hình chiếu vuông góc của $\large B'$ lên mặt phẳng $\large (ABC)$ trùng với trọng tâm tam giác $\large ABC$. Tính thể tích khối tứ diện $\large A'ABC$ theo $\large a$

• A.

  A. $\large\frac{3a^{3}}{26}$

• B.

  B. $\large\frac{9a^{3}}{26}$

• C.

  C. $\large\frac{27a^{3}}{208}$

• D.

  D. $\large\frac{9a^{3}}{208}$

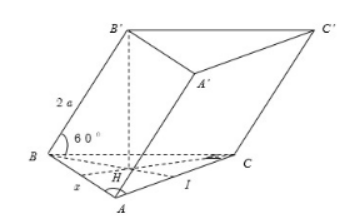
Gọi $\large H$ là trọng tâm tam giác $\large ABC,I$ là trung điểm cạnh $\large AC$.

Theo giả thiết ta có $\large B'H\perp(ABC) \Rightarrow\left(BB',(ABC)\right)=\widehat{B'BH}=60^{\circ}$

Trong tam giác vuông $\large B'BH$ có:

$\large B'H=BB'\cdot \sin 60^{\circ}=2a\cdot \frac{\sqrt{3}}{2}=a\sqrt{3}$

$\large BH=BB'\cdot \cos 60^{\circ}=2a.\frac{1}{2}=a\Rightarrow BI=\frac{3}{2} BH=\frac{3a}{2}$

Giả sử $\large AB=x,x>0 \Rightarrow AC=AB\cdot \cos \widehat{BAC}=x\cdot \cos 60^{\circ}=\frac{x}{2};BC=AB\cdot \sin 60^{\circ}=\frac{x\sqrt{3}}{2}$

Áp dụng định lý cosin trong tam giác $\large ABI$, ta có $\large BI^{2}=AB^{2}+AI^{2}-2AB \cdot AI \cdot \cos 60^{\circ} \Leftrightarrow \frac{9a^{2}}{4}=x^{2}+\left(\frac{x}{4}\right)^{2}-2 x \cdot \frac{x}{4} \cdot \frac{1}{2} \Leftrightarrow x^{2}=\frac{36 a^{2}}{13}$

Diện tích tam giác $\large ABC$ là $\large S=\frac{1}{2}\cdot CA.CB=\frac{1}{2} \cdot \frac{x}{2} \cdot \frac{x \sqrt{3}}{2}=\frac{x^{2}\sqrt{3}}{8}=\frac{9 a^{2} \sqrt{3}}{26}$

Vậy thể tích khối tứ diện $\large A'ABC$ là $\large V=\frac{1}{3}.S_{ABC}=B'H=\frac{1}{3}\cdot \frac{9a^{2}\sqrt{3}}{26}\cdot a\sqrt{3}=\frac{9a^{3}}{26}$

Đáp án B