Cho tam giác OABOAB đều cạnh aa. Trên đường thẳng $\larg
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho tam giác OABOAB đều cạnh aa. Trên đường thẳng dd qua OO và vuông góc với mặt phẳng (OAB)(OAB) lấy điểm MM sao cho OM=xOM=x. Gọi E,FE,F lần lượt là hình chiếu vuông góc của AA trên MBMB và OBOB. Gọi NN là giao điểm của EFEF và dd. Tìm xx để thể tích tứ diện ABMNABMN có giá trị nhỏ nhất.
Đáp án án đúng là: B
Lời giải chi tiết:
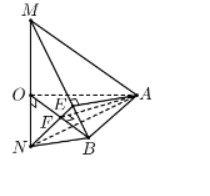
Đặt ON=y>0ON=y>0. Khi đó:
VABMN=VABOM+VABON=13S△OAB(OM+ON)=13⋅a2√34(x+y)VABMN=VABOM+VABON=13S△OAB(OM+ON)=13⋅a2√34(x+y)
Ta có {AF⊥OBAF⊥MO⇒AF⊥(MOB) ⇒AF⊥MB
Lại có MB⊥AE nên suy ra MB⊥(AEF)⇒MB⊥EF
Suy ra △OBM đồng dạng △ONF nên OBOM=ONOF⟶ON=OB⋅OFOM=a22x
Suy ra VABMN=a2√312(x+a22x)≥a3√612
Dấu "=" xảy ra ⇔x=a22x⇒x=a√22
Đáp án B
Xem thêm các bài tiếp theo bên dưới
- Một hộp không nắp được làm từ một mảnh cactong theo hình vẽ. Hộp có đá
- Để thiết kế một chiếc bể cá hình chữ nhật không nắp có chiều cao là 60
- Cho hình hộp ABCD.A′B′C′D′ có đáy ABCD là hình thoi
- Một viên đá dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng $\l
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật vớ