Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình chữ nhật vớ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình chữ nhật với AB=a,BD=a√3AB=a,BD=a√3 . Mặt bên SABSAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi MM là điểm thuộc cạnh SDSD sao cho MD=2MSMD=2MS. Tính theo aa khoảng cách hh giữa hai đường thẳng ADAD và MCMC.
Đáp án án đúng là: D
Lời giải chi tiết:
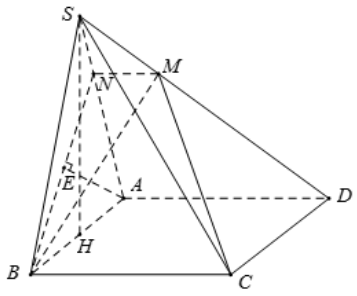
Trong tam giác SADSAD, kẻ MN//DA(N∈SA)MN//DA(N∈SA)
Ta có {AD⊥SHAD⊥AB{AD⊥SHAD⊥AB ⇒AD⊥(SAB)⇒MN⊥(SAB)
Khi đó: {AE⊥MN⊂(MBC)AE⊥BN⊂(MBC) ⇒AE⊥(MBC)⇒d(A,(MBC))=AE
Ta có: NASA=MDSD=23⇒SBNA=23SBAS=23⋅a2√34=a2√36
Áp dụng định lý cosin trong tam giác NBA, ta có
BN2=AB2+AN2−2AB⋅AN⋅cos^NAB=a2+4a29−2⋅a⋅2a3cos60∘=7a29⇒BN=a√73
Suy ra AE=2SBNABN=2⋅a2√36a√73=a√217 Vậy h=d(A,(MBC))=a√217
Đáp án D
Xem thêm các bài tiếp theo bên dưới