Cho hình lập phương $\large ABCD.A'B'C'D'$ cạnh $\large a$. Tính góc t

Cho hình lập phương $\large ABCD.A'B'C'D'$ cạnh $\large a$. Tính góc tạo bởi hai mặt phẳng $\large (BA'C)$ và $\large (DA'C)$

• A.

  A. $\large 30^{\circ}$

• B.

  B. $\large 45^{\circ}$

• C.

  C. $\large 60^{\circ}$

• D.

  D. $\large 90^{\circ}$

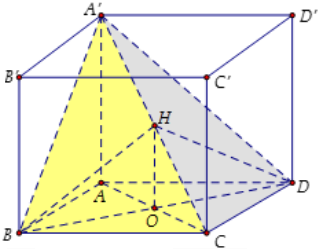
Gọi $\large O$ là tâm của hình vuông $\large ABCD$

Dựng $\large OH\perp A'C\left(H\in A'C\right)$

Khi đó $\large\left.\begin{align}A'C\perp OH\\A'C\perp BD\end{align}\right\} $ $\large\Rightarrow A'C\perp(BDH)$

Vậy $\large\widehat{\left(\left(BA'C\right),\left(DA'C\right)\right)}= \widehat{(HB,HD)}$

Trong tam giác vuông $\large A'BC$ có $\large BH=\frac{2S_{A'BC}}{A'C}=\frac{BC\cdot A'B}{A'C}=\frac{a\cdot a \sqrt{2}}{a\sqrt{3}}=\frac{a\sqrt{6}}{3}$

Tương tự ta có $\large DH=\frac{a\sqrt{6}}{3}$

Trong tam giác $\large BHD$, áp dụng định lý cosin ta có $\large\widehat{BHD}=\frac{BH^{2}+DH^{2}-BD^{2}}{2BH \cdot DH}$

$\large =\frac{\frac{2a^{2}}{3}+\frac{2a^{2}}{3}-2a^{2}}{2\cdot \frac{2a^{2}}{3}}=-\frac{1}{2}$

Suy ra $\large\widehat{BHD}=120^{0} \Rightarrow\widehat{(HB,HD}=60^{\circ}$

Vậy $\large\widehat{\left(\left(BA'C\right),\left(DA'C\right)\right)}=60^{\circ}$

Đáp án C