Cho hình chóp $\large S.ABCD$ có đáy là hình chữ nhật với $\large AB=4

Cho hình chóp $\large S.ABCD$ có đáy là hình chữ nhật với $\large AB=4$. Cạnh bên $\large SA$ vuông góc với mặt phẳng đáy và $\large SC=6$. Thể tích lớn nhất của khối chóp đã cho bằng

• A.

  A. 24

• B.

  B. $\large\frac{20}{3}$

• C.

  C. $\large\frac{40}{3}$

• D.

  D. $\large\frac{80}{3}$

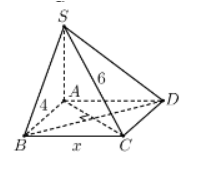
Đặt $\large BC=x$ suy ra $\large AC=\sqrt{16+x^{2}}$ và $\large SA=\sqrt{20-x^{2}}$ . Đk $\large 0

Thể tích khối chóp $\large V_{S.ABCD}=\frac{1}{3}S_{ABCD}.SA=\frac{4}{3}x\sqrt{20-x^{2}}$

$\large\leq \frac{4}{3} \cdot \frac{x^{2}+\left(\sqrt{20-x^{2}}\right)^{2}}{2}=\frac{40}{3}$

Dấu "=" xảy ra $\large\Leftrightarrow x=\sqrt{20-x^{2}} \Leftrightarrow x=\sqrt{10}$

Đáp án C