Cho tứ diện $\large SABC$ có trọng tâm $\large G$. Một mặt phẳng qua $

Cho tứ diện $\large SABC$ có trọng tâm $\large G$. Một mặt phẳng qua $\large G$ cắt các tia $\large SA,SB,SC$ theo thứ tự tại $\large A',B',C'$. Đặt $\large\frac{SA'}{SA}=m, \frac{SB'}{SB}=n, \frac{SC'}{SC}=p$. Đẳng thức nào sau đây đúng

• A.

  A. $\large\frac{1}{mn}+\frac{1}{np}+\frac{1}{pm}=4$

• B.

  B.  $\large\frac{1}{m}+\frac{1}{n}+\frac{1}{p}=4$

• C.

  C. $\large m+n+p=4$

• D.

  D. $\large\frac{1}{m^{2}}+\frac{1}{n^{2}}+\frac{1}{p^{2}}=1$

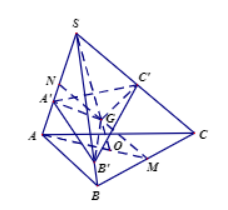
Gọi $\large M,N$ lần lượt là trung điểm các cạnh $\large BC,SA,O$ là trọng tâm tam giác $\large ABC$

Khi đó, ta có $\large\left \{G \right \}=MN \cap SO$

Xét tam giác $\large SAM$ có $\large\overrightarrow{SG}=\frac{1}{2}\left ( \overrightarrow{SN}+\overrightarrow{SM} \right )=\frac{1}{2}\left ( \frac{1}{2}\overrightarrow{SA}+\overrightarrow{SM} \right )=\frac{1}{4}\left ( \overrightarrow{SA}+2\overrightarrow{SM} \right )$

Và $\large\overrightarrow{SO}=\frac{1}{3}\overrightarrow{SA}+\frac{2}{3}\overrightarrow{SM}=\frac{1}{3}\left ( \overrightarrow{SA}+2\overrightarrow{SM} \right )=\frac{4}{3}\overrightarrow{SG}\Rightarrow \frac{SG}{SO}=\frac{3}{4}$

Ta có $\large\frac{V_{SA'GC'}}{V_{SAOC}}=\frac{SA'}{SA}.\frac{SG}{SO}.\frac{SC'}{SC}=m.\frac{3}{4}.p\Rightarrow V_{SA'GC'}=\frac{3}{4}mnp.\frac{V_{SAOC}}{n}$ (1)

$\large\frac{V_{SA'GB'}}{V_{SAOB}}=\frac{SA'}{SA}.\frac{SG}{SO}.\frac{SB'}{SB}=m.\frac{3}{4}.n\Rightarrow V_{SA'GB'}=\frac{3}{4}mnp.\frac{V_{SAOB}}{p}$ (2)

$\large\frac{V_{S.B'GC'}}{V_{S.BOC}}=\frac{SB'}{SB}.\frac{SG}{SO}.\frac{SC'}{SC}=n\cdot \frac{3}{4}\cdot p\Rightarrow V_{S.B'GC'}=\frac{3}{4}mnp.\frac{V_{S.BOC}}{m}$ (3)

Cộng (1), (2), (3) vế theo vế ta được:

$\large V_{S.A'B'C'}=\frac{3}{4} mnp\left(\frac{1}{n} \cdot V_{S.AOC}+\frac{1}{p} \cdot V_{S.AOB}+\frac{1}{m} \cdot V_{S.BOC}\right)$

$\large\Leftrightarrow \frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{3}{4} mnp\left(\frac{1}{n} \cdot \frac{V_{S.AOC}}{V_{S.ABC}}+\frac{1}{p} \cdot \frac{V_{S.AOB}}{V_{S.ABC}}+\frac{1}{m} \cdot \frac{V_{S.BOC}}{V_{S.ABC}}\right)$

$\large\Leftrightarrow mnp=\frac{3}{4} mnp\left(\frac{1}{n} \cdot \frac{S_{AOC}}{S_{ABC}}+\frac{1}{p} \cdot \frac{S_{AOB}}{S_{ABC}}+\frac{1}{m} \cdot \frac{S_{BOC}}{S_{ABC}}\right)$

$\large\Leftrightarrow \frac{4}{3}=\left[\frac{1}{n}.\frac{d(O;AC)}{d(B;AC)}+\frac{1}{p}\cdot \frac{d(O;AB)}{d(C;AB)}+\frac{1}{m}\cdot \frac{d(O;BC)}{d(A;BC)}\right] \Leftrightarrow \frac{4}{3}=\frac{1}{n} \cdot \frac{1}{3}+\frac{1}{p} \cdot \frac{1}{3}+\frac{1}{m} \cdot \frac{1}{3}$

$\large\Leftrightarrow \frac{1}{m}+\frac{1}{n}+\frac{1}{p}=4$

Bình luận: Nếu làm trắc nghiệm, ta chọn mặt phẳng qua $\large O$ và cắt $\large SA,SB,SC$ là mặt phẳng $\large (NBC)$, ta có ngay đáp án $\large\frac{1}{m}+\frac{1}{n}+\frac{1}{p}=4$

Đáp án B