Cho lăng trụ $\large ABC.A'B'C'$ có thể tích bằng $\large V$. Các điểm

Cho lăng trụ $\large ABC.A'B'C'$ có thể tích bằng $\large V$. Các điểm $\large M,N,E$ lần lượt nằm trên các cạnh $\large A'B',A'C',AB$ sao cho $\large M'A=3MB',NA'=NC',EB=3EA$. Mặt phẳng $\large (MNE)$ cắt $\large AC$ tại $\large F$. Thể tích khối đa diện lồi $\large BEFCC'MN$ bằng

• A.

  A. $\large\frac{3}{8}V$

• B.

  B. $\large\frac{41}{72}V$

• C.

  C. $\large\frac{53}{72}V$

• D.

  D. $\large\frac{5}{24}V$

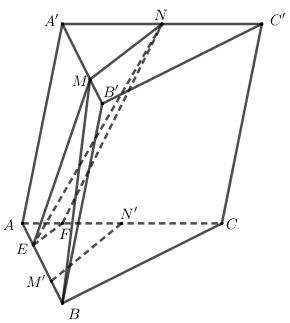
Ta có $\large (ABC)//(A'B'C')$

Mà $\large (M N) \cap\left(A B^{\prime} C^{\prime}\right)=MN; (MNE) \cap(A B C)=E F \Rightarrow E F / / M N$

Do đó hình đa diện $\large A'MNAEF$ là hình chóp cụt 

Gọi $\large h$ là chiều cao khối lăng trụ. $\large S$ là diện tích đáy của hình lăng trụ

Ta có $\large\frac{S_{A'MN}}{S_{A'B'C'}}=\frac{A'M}{A'B'}.\frac{A'N}{A'C'}=\frac{3}{4}.\frac{1}{2}\Rightarrow S_{A'MN}=\frac{3}{8}S$

Trong (ABC), lấy M', N' sao cho 4M'B=AB và N'A=N'C $\large \Rightarrow M'N'//MN//EF$

Ta có $\large 4AE=AB=4M'B\Rightarrow AE=M'B\Rightarrow AE=\frac{1}{3}AM'\Rightarrow AF=\frac{1}{3}AN'=\frac{1}{6}AC$

$\large\frac{S_{AEF}}{S_{ABC}}=\frac{AE}{AB}.\frac{AF}{AC}=\frac{1}{4}.\frac{1}{6}=\frac{1}{24}\Rightarrow S_{AEF}=\frac{1}{24}S$

Thể tích hình chóp cụt $\large A'MNAEF$ là 

$\large V_{A'MN.AEF}=\frac{1}{3}(S_{A'MN}+S_{AEF}+\sqrt{S_{A'MN}.S_{AEF}}).h=\frac{1}{3}(\frac{3}{8}S+\frac{1}{24}S+\sqrt{\frac{3}{8}S.\frac{1}{24}S}).h=\frac{13}{72}S.h=\frac{13}{72}V$

Ta lại có $\large\frac{S_{B'C'M}}{S_{B'C'A'}}=\frac{B'C'}{B'C'}.\frac{B'M}{B'A'}=\frac{1}{4}\Rightarrow S_{B'C'M}=\frac{1}{4}S$

Thể tích khối chóp $\large B.B'C'M$ là $\large V_{B.B'CM}=\frac{1}{3}.\frac{1}{4}S.h=\frac{1}{12}V$

Thể tích khối đa diện $\large BEFCC'MN$ là: $\large V-(\frac{13}{73}V+\frac{1}{12}V)=\frac{53}{72}V$

Đáp án C