Cho tứ diện đều $\Large ABCD$ có cạnh $\Large a$. Gọi $\Large M$ là tr

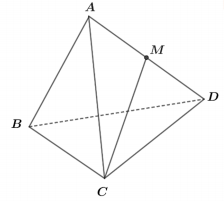
Cho tứ diện đều $\Large ABCD$ có cạnh $\Large a$. Gọi $\Large M$ là trung điểm của cạnh $\Large AD$ ( tham khảo hình vẽ dưới). Tính khoảng cách giữa $\Large AB$ và $\Large CM$ theo $\Large a$.

• A.

  $\Large \dfrac{a\sqrt{33}}{11}$.

• B.

  $\Large \dfrac{a}{\sqrt{33}}$.

• C.

  $\Large \dfrac{a}{\sqrt{22}}$.

• D.

  $\Large \dfrac{a\sqrt{22}}{11}$.

Chọn D

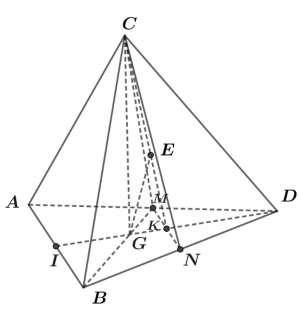
Gọi $\Large G$ là trọng tâm $\Large \Delta ABD$. Vì $\Large ABCD$ là tứ diện đều nên $\Large CG\perp (ABD)$.

Gọi $\Large I, N, K$ lần lượt là trung điểm của $\Large AB, BD, MN$ $\Large \Rightarrow MN // AB \Rightarrow AB // (CMN)$.

$\Large \Rightarrow d(AB, CM)=d\left(AB, (CMN)\right)=d\left(I, (CMN)\right)=3d\left(G, (CMN)\right)$.

Gọi $\Large E$ là hình chiếu của $\Large G$ lên $\Large CK$.

Ta có $\Large \left\{\begin{align} & MN\perp GK \\ & MN\perp CG \end{align}\right.$ $\Large \Rightarrow MN\perp (CKG)\Rightarrow MN\perp GE$ (1)

Mà $\Large GE\perp CK$ (2)

Từ (1) và (2) suy ra $\Large GE\perp (CMN)\Rightarrow d\left(G, (CMN)\right)=GE$.

Ta có $\Large GK=\dfrac{1}{6}DI=\dfrac{a\sqrt{3}}{12}$;

$\Large CG^2=CB^2-BG^2$ $\Large =a^2-\left(\dfrac{a\sqrt{3}}{3}\right)^2=\dfrac{2}{3}a^2$.

Xét tam giác vuông $\Large CGK$: $\Large \dfrac{1}{GE^2}=\dfrac{1}{GC^2}+\dfrac{1}{GK^2}$ $\Large =\dfrac{3}{2a^2}+\dfrac{144}{3a^2}=\dfrac{99}{2a^2}$.

$\Large \Rightarrow GE=\dfrac{a\sqrt{2}}{3\sqrt{11}}$ $\Large \Rightarrow d(CM, AB)=3.\dfrac{a\sqrt{2}}{3\sqrt{11}}=\dfrac{a\sqrt{22}}{11}$.