Cho hình nón đỉnh $\Large S$ và đáy là hình tròn tâm $\Large O$. Biết

Cho hình nón đỉnh $\Large S$ và đáy là hình tròn tâm $\Large O$. Biết rằng chiều cao hình nón bằng $\Large a$ và bán kính đáy của hình nón bằng $\Large 2a$. Một mặt phẳng $\Large (P)$ đi qua đỉnh $\Large S$ và cắt đường tròn đáy nón tại hai điểm $\Large A, B$ mà $\Large AB=2a\sqrt{3}$. Hãy tính theo $\Large a$ diện tích mặt cầu ngoại tiếp khối tứ diện $\Large SOAB$.

• A.

  $\Large 5\pi a^2$.

• B.

  $\Large 17\pi a^2$.

• C.

  $\Large 7\pi a^2$.

• D.

  $\Large 26\pi a^2$.

Chọn B

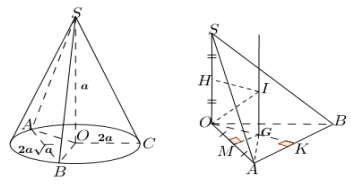
Gọi $\Large G$ là giao điểm ba đường trung trực của $\Large \Delta OAB$, suy ra $\Large G$ là tâm đường tròn ngoại tiếp $\Large \Delta OAB$. Từ $\Large G$ dựng đường thẳng vuông góc đáy, $\Large HI$ là trung trực $\Large SO$ và cắt đường thẳng dựng từ $\Large G$ tại $\Large I$. Khi đó ta có $\Large R_{SOAB}=IA=IO=IB=IC$.

Ta có $\Large OM=\dfrac{OA}{2}=a$. $\Large \Delta OMG \sim \Delta OKB$ $\Large \Rightarrow \dfrac{OG}{OB}=\dfrac{OM}{OK}$ $\Large \Rightarrow OG=\dfrac{OM.OB}{OK}=\dfrac{a.2a}{a}=2a$.

$\Large IG=HO=\dfrac{SO}{2}=\dfrac{a}{2}$ $\Large \Rightarrow IO=\sqrt{IG^2+OG^2}=\sqrt{\dfrac{a^2}{4}+4a^2}=\dfrac{a\sqrt{17}}{2}$.

Khi đó mặt cầu ngoại tiếp tứ diện $\Large SOAB$ bằng $\Large S=4\pi R^2=4\pi IO^2$ $\Large =4\pi .\dfrac{17a^2}{4}=17\pi a^2$.