Xét hàm số $\Large f(x)=\left|\dfrac{mx-2\sqrt{x+4}}{2x+4}\right|$ với

Xét hàm số $\Large f(x)=\left|\dfrac{mx-2\sqrt{x+4}}{2x+4}\right|$ với $\Large m$ là tham số thực. Có bao nhiêu số nguyên của $\Large m$ thỏa mãn điều kiện $\Large 0 < \underset{[-1; 1]}{min}f(x) < 1$.

• A. 4.
• B. 8.
• C. 12.
• D. 1.

Chọn B
Hàm số $\Large g(x)=\dfrac{mx-2\sqrt{x+4}}{2x+4}$ là hàm liên tục trên đoạn [-1; 1], nếu $\Large \exists x_0\in [-1; 1]$ sao cho $\Large g(x_0)=0$ thì $\Large \underset{[-1; 1]}{min}f(x)=0$ không thỏa mãn yêu cầu bài toán, vậy điều kiện cần là phương trình $\Large \dfrac{mx-2\sqrt{x+4}}{2x+4}=0$ $\Large \Leftrightarrow mx-2\sqrt{x+4}=0$ (1) vô nghiệm trên đoạn [-1; 1].

Đặt $\Large \sqrt{x+4}=t$ $\Large \Rightarrow t\in [\sqrt{3}; \sqrt{5}]$ khi đó (1) $\Large \Leftrightarrow m(t^2-4)-2t=0$ $\Large \Leftrightarrow m=\dfrac{2t}{t^2-4}$ (Do $\Large t=2$ không là nghiệm của phương trình)

Xét hàm số $\Large y=\dfrac{2t}{t^2-4}$ trên $\Large [\sqrt{3}; \sqrt{5}]\setminus \begin{Bmatrix} 2 \end{Bmatrix}$. $\Large y'=\dfrac{-2t^2-8}{(t^2-4)^2} < 0$ $\Large \forall t\in [\sqrt{3}; \sqrt{5}]\setminus \begin{Bmatrix} 2 \end{Bmatrix}$ nên có BBT:

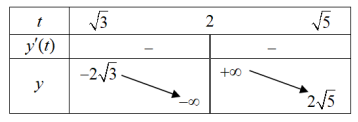
(1) vô nghiệm trên đoạn [-1; 1] $\Large \Leftrightarrow m=\dfrac{2t}{t^2-4}$ vô nghiệm trên $\Large [\sqrt{3}; \sqrt{5}]$ $\Large \Leftrightarrow -2\sqrt{3} < m < 2\sqrt{5}$

Ngược lại khi $\Large -2\sqrt{3} < m < 2\sqrt{5}$ hàm số $\Large g(x)=\dfrac{mx-2\sqrt{x+4}}{2x+4}$ luôn có $\Large g(0)=-1$, nếu hàm số đạt cực tiểu tại $\Large x=0$ thì $\Large g'(0)=\dfrac{4m+6}{(2x+4)^2}$ $\Large \Rightarrow g'(0)=0$ $\Large \Leftrightarrow m=-\dfrac{3}{2}$ thì $\Large m$ không nguyên, nên khi $\Large m$ nguyên hàm số không đạt cực trị tại $\Large x=0$, cùng với tính liên tục của hàm số trên đoạn [-1; 1] ta suy ra $\Large \exists x_0\in [-1; 1]$: $\Large -1 < g(x_0) < 0$ $\Large \Rightarrow \underset{[-1; 1]}{min}f(x) < 1$.

Vậy điều kiện cần và đủ để $\Large 0 < \underset{[-1; 1]}{min}f(x) < 1$ là $\Large -2\sqrt{3} < m < 2\sqrt{5}$ và trên tập số nguyên thì $\Large m\in \begin{Bmatrix} -3; -2; -1; 0; 1; 2; 3; 4 \end{Bmatrix}$ nên có 8 giá trị nguyên của $\Large m$ thỏa mãn yêu cầu bài toán.