Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình thoi

Cho hình hộp $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình thoi tâm $\Large O$ và cạnh bằng $\Large a$, $\Large \widehat{BAC}=60^{\circ}$. Gọi $\Large I, J$ lần lượt là tâm của các mặt bên $\Large ABB'A', CDD'C'$. Biết $\Large AI=\dfrac{a\sqrt{7}}{2}$, $\Large AA'=2a$ và góc giữa hai mặt phẳng $\Large (ABB'A')$, $\Large (A'B'C'D')$ bằng $\Large 60^{\circ}$. Tính theo $\Large a$ thể tích của khối tứ diện $\Large AOIJ$.

• A.

  $\Large \dfrac{3\sqrt{3}a^3}{64}$.

• B.

  $\Large \dfrac{\sqrt{3}a^3}{48}$.

• C.

  $\Large \dfrac{\sqrt{3}a^3}{32}$.

• D.

  $\Large \dfrac{\sqrt{3}a^3}{192}$.

Chọn C

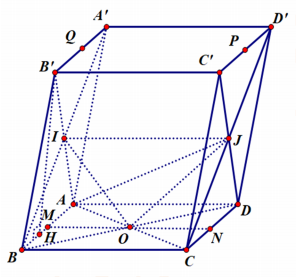
+) Ta có $\Large ABCD$ là hình thoi, $\Large \widehat{BAC}=60^{\circ}$ $\Large \Rightarrow \Delta ABC$ là tam giác đều.

$\Large \Rightarrow AC=a, BO=OD=\dfrac{a\sqrt{3}}{2}$ $\Large \Rightarrow BD=a\sqrt{3}$ $\Large \Rightarrow S_{ABCD}=\dfrac{1}{2}AC.BD=\dfrac{a^2\sqrt{3}}{2}$.

+) $\Large AI=\dfrac{a\sqrt{7}}{2}$ $\Large \Rightarrow AB'=a\sqrt{7}$ $\Large \Rightarrow cos\widehat{BAB'}=\dfrac{AB^2+(AB')^2-(BB')^2}{2.AB.AB'}=\dfrac{2}{\sqrt{7}}$ $\Large \Rightarrow sin\widehat{BAB'}=\dfrac{\sqrt{3}}{\sqrt{7}}$

+) Kẻ $\Large B'H\perp AB$, xét $\Large \Delta AHB'$ có $\Large sin\widehat{BAB'}=\dfrac{B'H}{AB'}$ $\Large \Rightarrow HB'=AB'.sin\widehat{BAB'}=a\sqrt{3}$. Suy ra $\Large d\big(B', (ABCD)\big)=AB'.sin60^{\circ}=\dfrac{3a}{2}$.

+) Mà $\Large S_{OIJ}=\dfrac{1}{2}S_{MNIJ}=\dfrac{1}{4}S_{MNPQ}=\dfrac{1}{4}S_{BCC'B'}$, $\Large d\big(A, (MNPQ)\big)=\dfrac{1}{2}d\big(A, (BCC'B')\big)$

Suy ra $\Large V_{AOIJ}=\dfrac{1}{8}V_{ABB'C'C}=\dfrac{1}{24}V_{ABCD.A'B'C'D'}$ mà $\Large V_{ABCD.A'B'C'D'}=d\big(B', (ABCD)\big).S_{ABCD}=\dfrac{3\sqrt{3}a^3}{4}$

$\Large \Rightarrow V_{AOIJ}=\dfrac{1}{24}V_{ABCD.A'B'C'D'}=\dfrac{a^3\sqrt{3}}{32}$.