Cho tứ diện đều $\Large ABCD$ có cạnh bằng $\Large a$, $\Large M$ là t

Cho tứ diện đều $\Large ABCD$ có cạnh bằng  $\Large a$, $\Large M$ là trung điểm cạnh $\Large CD$. Tính cosin của góc giữa hai đường thẳng $\Large AC,\,BM$.

• A. $\Large \dfrac{\sqrt{3}}{6}$.
• B. $\Large \dfrac{\sqrt{3}}{2}$.
• C. $\Large 0$
• D. $\Large \dfrac{2\sqrt{3}}{3}$.

Chọn    A.
 

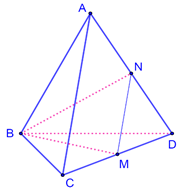
Gọi $\Large N$ là trung điểm của $\Large AD$$\Rightarrow MN\text{//}AC$.
Khi đó $\Large \cos \left( AC;BM \right)=\cos \left( MN;BM \right)=\left| \cos \widehat{BMN} \right|$.
Xét $\Large \Delta BMN$ có: $\Large BM=\dfrac{a\sqrt{3}}{2};BN=\dfrac{a\sqrt{3}}{2};MN=\dfrac{a}{2}$.
$\Large \Rightarrow \cos \widehat{BMN}=\dfrac{M{{N}^{2}}+B{{M}^{2}}-B{{N}^{2}}}{2.MN.BM}=\dfrac{{{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{a\sqrt{3}}{2} \right)}^{2}}-{{\left( \dfrac{a\sqrt{3}}{2} \right)}^{2}}}{2.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{2}}=\dfrac{\sqrt{3}}{6}$.
Vậy $\Large \cos \left( AC;BM \right)=\left| \dfrac{\sqrt{3}}{6} \right|=\dfrac{\sqrt{3}}{6}$.