Cho hình chóp S.ABCD có đáy là hình thang vuông tại $\Large A
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A,D, AD=CD=a;AB=2a,SA vuông góc với mặt phẳng đáy. Góc giữa cạnh bên SC và mặt phẳng (ABCD) bằng 45∘\Large . Gọi I là trung điểm của cạnh AB. Tính khoảng cách từ điểm I đến mặt phẳng (SBC).
Đáp án án đúng là: C
Lời giải chi tiết:
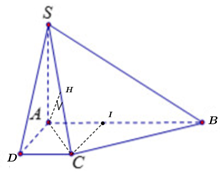
Ta có SA⊥(ABCD)⇒(SC,(ABCD))=(SC,CA)=^SCA=45∘
⇒ΔSAC vuông cân ở A ⇒SA=AC=a√2.
Kẻ AH⊥SC tại H.
Tứ giác ADCI có AIDC;AI=AD=DC=a;^DAI=90∘\Large nên nó là hình vuông.
Xét ΔACB có AI=IB=IC=a
Mà IC là trung tuyến ⇒ΔACI vuông ở C⇒CB⊥AC
Mặt khác CB⊥SA⇒CB⊥(SAC)⇒CB⊥HA
Vì CB⊥AHSC⊥AH}⇒AH⊥(SCB).
⇒d(A,(SCB))=AH.
Mà ΔSACvuông cân ở A⇒AH=a.
Vì I là trung điểm AB⇒d(I,(SBC))=12d(A,(SBC))=a2
Xem thêm các bài tiếp theo bên dưới