Cho hàm số bậc ba $\Large y=f\left( x \right)$ có đồ thị như hình dưới

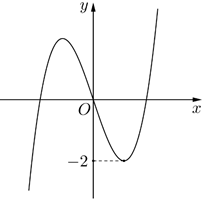
Cho hàm số bậc ba $\Large y=f\left( x \right)$ có đồ thị như hình dưới. Phương trình $\Large f\left( {{x}^{2}} \right)+1=0$ có bao nhiêu nghiệm?

• A. $\Large 0$.
• B. $\Large 3$.
• C. $\Large 4$.
• D. 3.

Từ đồ thị hàm số bậc ba $\Large y=f\left( x \right)$ suy ra $\Large f\left( x \right)=-1$$\Large \Leftrightarrow \left[ \begin{matrix}& x={{x}_{1}} \\ & x={{x}_{2}} \\ & x={{x}_{3}} \\ \end{matrix} \right.$ với $\Large {{x}_{1}}<0<{{x}_{2}}<{{x}_{3}}$
Ta có: $\Large f\left( {{x}^{2}} \right)+1=0$$\Large \Leftrightarrow f\left( {{x}^{2}} \right)=-1$$\Large \Leftrightarrow \left[ \begin{matrix}& {{x}^{2}}={{x}_{1}}\,\,\,\,\,\left( 1 \right) \\ &{{x}^{2}}={{x}_{2}}\,\,\,\,\left( 2 \right) \\ & {{x}^{2}}={{x}_{3}}\,\,\,\,\left( 3 \right) \\ \end{matrix} \right.$
Vì $\Large {{x}_{1}}<0<{{x}_{2}}<{{x}_{3}}$ nên phương trình $\Large \left( 1 \right)$ vô nghiệm; mỗi phương trình $\Large \left( 2 \right)$ và $\Large \left( 3 \right)$ có $\Large 2$ nghiệm phân biệt.
Vậy phương trình $\Large f\left( {{x}^{2}} \right)+1=0$ có $\Large 4$ nghiệm