Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABCD$ là hình vuông cạnh $\Large a$, $\Large SA=a$ và $\Large SA$ vuông góc với đáy. Gọi $\Large M$ là trung điểm của $\Large SB$, $\Large N$ thuộc cạnh $\Large SN=2ND$. Tính $\Large V$ của khối tứ diện $\Large ACMN$.

• A. $\Large V=\dfrac{1}{36}{{a}^{3}}$.
• B. $\Large V=\dfrac{1}{12}{{a}^{3}}$.
• C. $\Large V=\dfrac{1}{8}{{a}^{3}}$.
• D. $\Large V=\dfrac{1}{6}{{a}^{3}}$.

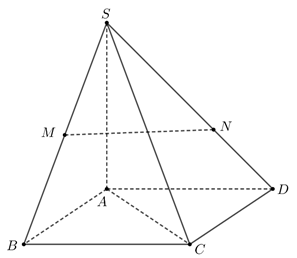
$\Large {{V}_{ACMN}}={{V}_{S.ABCD}}-{{V}_{SAMN}}-{{V}_{DNAC}}-{{V}_{BAMC}}-{{V}_{SMCN}}$. Ta có
$\Large \dfrac{{{V}_{SAMN}}}{{{V}_{SABD}}}=\dfrac{SM}{SB}.\dfrac{SN}{SD}=\dfrac{1}{3}\Rightarrow {{V}_{SAMN}}=\dfrac{1}{6}V{}_{SABCD}$
$\Large \dfrac{{{V}_{DACN}}}{{{V}_{DACS}}}=\dfrac{ND}{SD}=\dfrac{1}{3}\Rightarrow {{V}_{SAMN}}=\dfrac{1}{6}V{}_{SABCD}$
$\Large \dfrac{{{V}_{BACM}}}{{{V}_{BACS}}}=\dfrac{BM}{BS}=\dfrac{1}{2}\Rightarrow {{V}_{SAMN}}=\dfrac{1}{4}V{}_{SABCD}$
$\Large \dfrac{{{V}_{SMCN}}}{{{V}_{SBCD}}}=\dfrac{SM}{BS}.\dfrac{SN}{SD}=\dfrac{1}{3}\Rightarrow {{V}_{SAMN}}=\dfrac{1}{6}V{}_{SABCD}$
Vậy $\Large {{V}_{ACMN}}=\dfrac{1}{4}{{V}_{SABCD}}=\dfrac{1}{12}{{a}^{3}}$